并查集(Disjoint-Set)
简介并查集(Disjoint-Set)是一种可以动态维护若干个不重叠的集合,并支持合并与查询两种操作的一种数据结构。
4.13.1、并查集的定义
并查集(Disjoint-Set)是一种可以动态维护若干个不重叠的集合,并支持合并与查询两种操作的一种数据结构。
并查集可以高效地进行如下操作:
- 查询元素p和元素q是否属于同一组
- 合并元素p和元素q所在的组

4.13.2、并查集的结构
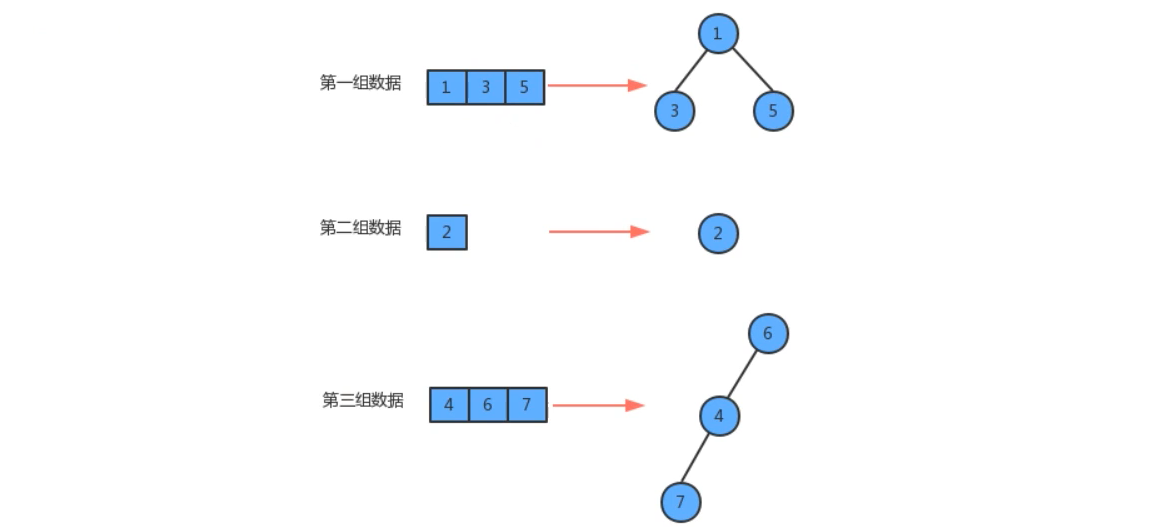
并查集也是一种树形结构,但这棵树跟我们前面学习的二叉树、红黑树、B树等都不一样,这种树的要求比较简单:
- 每个元素都唯一的对应一个结点
- 每一组数据中的多个元素都在同一棵树中
- 一个组中的数据对应的树和另一个组的数据对应的树之间没有任何联系
- 元素在树中并没有子父级关系的硬性要求
4.13.3、并查集API设计
| 类名 | UF |
|---|---|
| 构造方法 | UF(int N):初始化并查集,以整数标识(0,N-1)个结点 |
| 成员变量 | private int[] eleAndGroup:记录结点元素和该元素所在分组的标识 private int count:记录并查集中数据的分组个数 |
| 成员方法 | public int count():获取当前并查集中的数据有多少个分组 public boolean connected(int p,int q):判断并查集中元素p和q是否在同一个分组中 public int find(int p):元素p所在分组的标识符 public void union(int p,int q):把p元素所在分组和q元素所在分组合并 |
4.13.4、并查集实现
实现类
package cn.test.algorithm.datastruct;
public class UF {
//元素和组
private int[] eleAndGroup;
//组的个数
private int count;
public UF(int N) {
//初始化分组的数量
count = N;
//初始化eleAdnGroup数组
eleAndGroup = new int[N];
//初始化eleAndGroup的元素和所在分组的标识,让eleAndGroup数组的索引作为并查集的每个结点的元素,并且让每个索引处的值作为组标识
for (int i = 0; i < eleAndGroup.length; i++) {
eleAndGroup[i] = i;
}
}
//分组个数
public int count() {
return count;
}
//查找p元素的分组标识符
public int find(int p) {
return eleAndGroup[p];
}
//判断并查集元素p和q是否在一个分组中
public boolean connected(int p, int q) {
return find(p) == find(q);
}
//合并两个组的元素
public void union(int p, int q) {
if (connected(p, q)) {
return;
}
//找到p所在组的标识符
int pGroup = find(p);
//找到q所在组的标识符
int qGroup = find(q);
//合并组,让p所在组的所有元素的标识符变为q所在分组的标识符
for (int i = 0; i < eleAndGroup.length; i++) {
if (eleAndGroup[i] == pGroup) {
eleAndGroup[i] = qGroup;
}
}
//分组个数减1
count--;
}
}
测试类
package cn.test.algorithm.test;
import cn.test.algorithm.datastruct.UF;
import java.util.Scanner;
public class UFTest {
public static void main(String[] args) {
//创建并查集对象
UF uf = new UF(100);
//从控制台录入两个合并的元素,调用union进行合并,获取合并后的并查集的分组数是否减少和组是否一样
Scanner scanner = new Scanner(System.in);
while (true) {
System.out.println("请输入第一个要合并的元素:");
int p = scanner.nextInt();
System.out.println("请输入第二个要合并的元素:");
int q = scanner.nextInt();
//判断两个是否在同一个组
if (uf.connected(p, q)) {
System.out.println("(" + p + "," + q + ")两个元素在同一个分组了");
continue;
} else {
uf.union(p, q);
System.out.println("当前并查集中还有:" + uf.count() + "个分组");
}
}
}
}
运行结果
请输入第一个要合并的元素:
1
请输入第二个要合并的元素:
3
当前并查集中还有:99个分组
请输入第一个要合并的元素:
1
请输入第二个要合并的元素:
3
(1,3)两个元素在同一个分组了
请输入第一个要合并的元素:
1
请输入第二个要合并的元素:
2
当前并查集中还有:98个分组
请输入第一个要合并的元素:
1
请输入第二个要合并的元素:
2
(1,2)两个元素在同一个分组了
请输入第一个要合并的元素:
4.13.5、并查集存在的问题
上面我们实现了并查集,如果我们N非常大的情况下,我们如果要将所有的数据都存放在一个组,那么我们需要调用N-1次union方法。但是我们union方法的内部是通过for循环遍历的方式去修改组的标识,所以我们合并算法的时间复杂度为O(N^2),如果要解决大规模问题,它是不合适的,我们就需要对算法进行优化。
4.13.6、并查集算法优化
为了提升union算法的性能,我们需要重新设计find方法和union方法的实现,此时先需要对之前的数据结构中的eleAndGroup数组的含义进行重新定义:
- 仍然让eleAndGroup数组的索引作为某个结点的元素
- eleAndGroup[i]的值不再是当前结点所在分组的标识,而是该结点的父结点
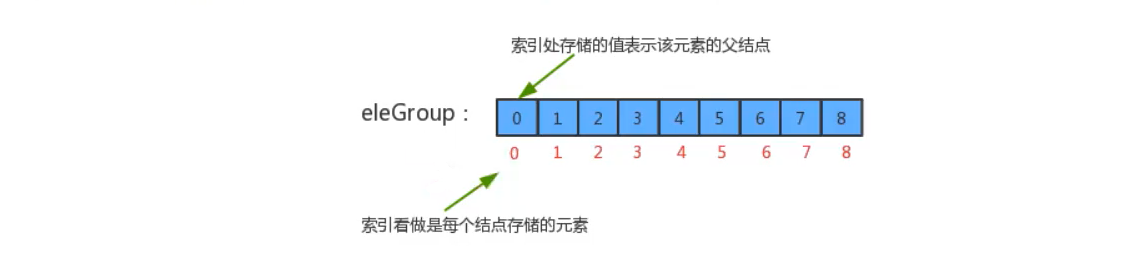
实现类
package cn.test.algorithm.datastruct;
public class UF_Tree {
//元素和组
private int[] eleAndGroup;
//组的个数
private int count;
public UF_Tree(int N) {
//初始化分组的数量
count = N;
//初始化eleAdnGroup数组
eleAndGroup = new int[N];
//初始化eleAndGroup的元素和所在分组的标识,让eleAndGroup数组的索引作为并查集的每个结点的元素,并且让每个索引处的值作为组标识
for (int i = 0; i < eleAndGroup.length; i++) {
eleAndGroup[i] = i;
}
}
//分组个数
public int count() {
return count;
}
//查找p元素的分组标识符
public int find(int p) {
while (true) {
if (p == eleAndGroup[p]) {
return p;
}
p = eleAndGroup[p];
}
}
//判断并查集元素p和q是否在一个分组中
public boolean connected(int p, int q) {
return find(p) == find(q);
}
//合并两个组的元素
public void union(int p, int q) {
//找到p所在组的标识符
int pRoot = find(p);
//找到q所在组的标识符
int qRoot = find(q);
//如果p和q在同一个分组就返回
if (pRoot == qRoot) {
return;
}
//让p所在树的根结点的父结点为q所在树的根节点即可
eleAndGroup[pRoot] = qRoot;
//分组个数减1
count--;
}
}
测试类
package cn.test.algorithm.test;
import cn.test.algorithm.datastruct.UF_Tree;
import java.util.Scanner;
public class UFTreeTest {
public static void main(String[] args) {
//创建并查集对象
UF_Tree uf = new UF_Tree(100);
//从控制台录入两个合并的元素,调用union进行合并,获取合并后的并查集的分组数是否减少和组是否一样
Scanner scanner = new Scanner(System.in);
while (true) {
System.out.println("请输入第一个要合并的元素:");
int p = scanner.nextInt();
System.out.println("请输入第二个要合并的元素:");
int q = scanner.nextInt();
//判断两个是否在同一个组
if (uf.connected(p, q)) {
System.out.println("(" + p + "," + q + ")两个元素在同一个分组了");
continue;
} else {
uf.union(p, q);
System.out.println("当前并查集中还有:" + uf.count() + "个分组");
}
}
}
}
测试结果
请输入第一个要合并的元素:
1
请输入第二个要合并的元素:
3
当前并查集中还有:99个分组
请输入第一个要合并的元素:
1
请输入第二个要合并的元素:
2
当前并查集中还有:98个分组
请输入第一个要合并的元素:
1
请输入第二个要合并的元素:
2
(1,2)两个元素在同一个分组了
请输入第一个要合并的元素:
上面我们优化过的并查集的union方法目前实现了O(1)的时间复杂度,但是里面我们调用了两次find方法,find方法中使用了while循环,这个最坏的情况下我们的时间复杂度还是O(n^2),所以我们目前优化的性能还是不是最好,那么下面我们在对它进行优化,使用路径压缩法。
4.13.7、路径压缩法
之前我们在union方法中,合并树的时候将任意的一棵树连接到了另外一棵树,这种合并方法是比较暴力的,如果我们把并查集每一棵树的大小记录下来,然后在每次合并树的时候,把较小的树连接到较大的树上,就可以减少数的深度。
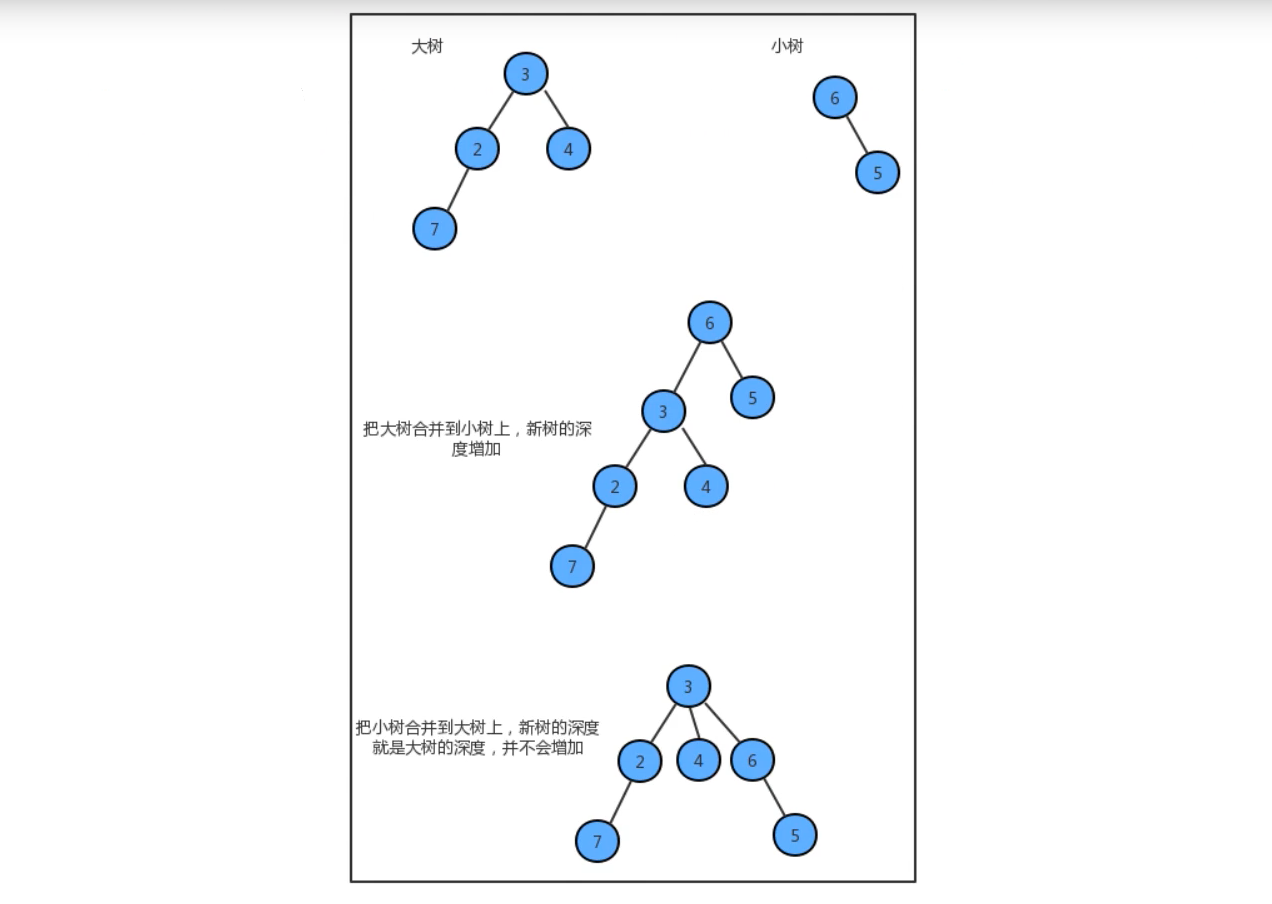
如果需要知道是大树还是小树,那么我们就需要用额外的数据来来存储这些树的成员个数了。这里我们api设计中需要新增一个变量:
//存储每个根结点对应的树中的元素个数
private int[] sz;
实现类
package cn.test.algorithm.datastruct;
public class UF_Tree_Weighted {
//元素和组
private int[] eleAndGroup;
//存在每个根结点对应树中的保存结点的个数
private int[] sz;
//组的个数
private int count;
public UF_Tree_Weighted(int N) {
//初始化分组的数量
count = N;
//初始化eleAdnGroup数组
eleAndGroup = new int[N];
sz = new int[N];
//初始化eleAndGroup的元素和所在分组的标识,让eleAndGroup数组的索引作为并查集的每个结点的元素,并且让每个索引处的值作为组标识
for (int i = 0; i < eleAndGroup.length; i++) {
eleAndGroup[i] = i;
sz[i] = 1;//默认情况下都是1
}
}
//分组个数
public int count() {
return count;
}
//查找p元素的分组标识符
public int find(int p) {
while (true) {
if (p == eleAndGroup[p]) {
return p;
}
p = eleAndGroup[p];
}
}
//判断并查集元素p和q是否在一个分组中
public boolean connected(int p, int q) {
return find(p) == find(q);
}
//合并两个组的元素
public void union(int p, int q) {
//找到p所在组的标识符
int pRoot = find(p);
//找到q所在组的标识符
int qRoot = find(q);
//如果p和q在同一个分组就返回
if (pRoot == qRoot) {
return;
}
//判断proot对应的大还是qroot对应的树大,最终需要把小的合并到大的上
if(sz[pRoot] < sz[qRoot]){
eleAndGroup[pRoot] = qRoot;
sz[qRoot] += sz[qRoot];
}else{
eleAndGroup[qRoot] = pRoot;
sz[pRoot] += sz[qRoot];
}
//分组个数减1
count--;
}
}
测试类
package cn.test.algorithm.test;
import cn.test.algorithm.datastruct.UF_Tree_Weighted;
import java.util.Scanner;
public class UFTreeWeightedTest {
public static void main(String[] args) {
//创建并查集对象
UF_Tree_Weighted uf = new UF_Tree_Weighted(100);
//从控制台录入两个合并的元素,调用union进行合并,获取合并后的并查集的分组数是否减少和组是否一样
Scanner scanner = new Scanner(System.in);
while (true) {
System.out.println("请输入第一个要合并的元素:");
int p = scanner.nextInt();
System.out.println("请输入第二个要合并的元素:");
int q = scanner.nextInt();
//判断两个是否在同一个组
if (uf.connected(p, q)) {
System.out.println("(" + p + "," + q + ")两个元素在同一个分组了");
continue;
} else {
uf.union(p, q);
System.out.println("当前并查集中还有:" + uf.count() + "个分组");
}
}
}
}
测试结果
请输入第一个要合并的元素:
1
请输入第二个要合并的元素:
3
当前并查集中还有:99个分组
请输入第一个要合并的元素:
1
请输入第二个要合并的元素:
3
(1,3)两个元素在同一个分组了
请输入第一个要合并的元素:
1
请输入第二个要合并的元素:
2
当前并查集中还有:98个分组
请输入第一个要合并的元素:
1
请输入第二个要合并的元素:
4
当前并查集中还有:97个分组
请输入第一个要合并的元素:
 前一篇博客中已经说过Golang对Gzip的处理,其实这是我的服务器端的处理,那么当我们服务器返回Gzip压缩的字符串后,客户端如何进行解压呢?本文主要记录下JavaScript对Gzip进行压缩和解压处理。
前一篇博客中已经说过Golang对Gzip的处理,其实这是我的服务器端的处理,那么当我们服务器返回Gzip压缩的字符串后,客户端如何进行解压呢?本文主要记录下JavaScript对Gzip进行压缩和解压处理。 Tauri 是一个框架,用于为所有主要桌面平台构建小巧、快速的二进制文件。开发人员可以集成任何可编译为 HTML、JS 和 CSS 的前端框架,以构建他们的用户界面。应用程序的后端是一个基于 Rust 的二进制文件,带有一个前端可以与之交互的 API。
Tauri 应用程序的用户界面目前在 macOS 和 Windows 上利用 tao 作为窗口处理库,在 Linux 上通过 Tauri 团队孵化和维护的 WRY 利用 WebKit、Windows 上的 WebView2 和 Linux 上的 WebKitGTK 创建一个统一的系统 webview(和其他好东西,如菜单和任务栏)接口。
Tauri 是一个框架,用于为所有主要桌面平台构建小巧、快速的二进制文件。开发人员可以集成任何可编译为 HTML、JS 和 CSS 的前端框架,以构建他们的用户界面。应用程序的后端是一个基于 Rust 的二进制文件,带有一个前端可以与之交互的 API。
Tauri 应用程序的用户界面目前在 macOS 和 Windows 上利用 tao 作为窗口处理库,在 Linux 上通过 Tauri 团队孵化和维护的 WRY 利用 WebKit、Windows 上的 WebView2 和 Linux 上的 WebKitGTK 创建一个统一的系统 webview(和其他好东西,如菜单和任务栏)接口。 OpenCV的全称是Open Source Computer Vision Library,是一个跨平台的计算机视觉处理开源软件库,是由Intel公司俄罗斯团队发起并参与和维护,支持与计算机视觉和机器学习相关的众多算法,以BSD许可证授权发行,可以在商业和研究领域中免费使用。OpenCV可用于开发实时的图像处理、计算机视觉以及模式识别程序,该程序库也可以使用英特尔公司的IPP进行加速处理。
OpenCV的全称是Open Source Computer Vision Library,是一个跨平台的计算机视觉处理开源软件库,是由Intel公司俄罗斯团队发起并参与和维护,支持与计算机视觉和机器学习相关的众多算法,以BSD许可证授权发行,可以在商业和研究领域中免费使用。OpenCV可用于开发实时的图像处理、计算机视觉以及模式识别程序,该程序库也可以使用英特尔公司的IPP进行加速处理。 《康熙王朝》是一部非常优秀的电视连续剧,陈道明演的康熙是我觉得最有帝王气魄,让人意犹未尽,本文主要记录一小段非常经典的对白。
《康熙王朝》是一部非常优秀的电视连续剧,陈道明演的康熙是我觉得最有帝王气魄,让人意犹未尽,本文主要记录一小段非常经典的对白。 快速生成表格
快速生成表格 Electron页面跳转、浏览器打开链接和打开新窗口
Electron页面跳转、浏览器打开链接和打开新窗口 在使用Git的过程中,不想每次都输入用户名和密码去拉取代码,所以就需要保存这些信息,那么既然有保存了,就必须有清除功能。
在使用Git的过程中,不想每次都输入用户名和密码去拉取代码,所以就需要保存这些信息,那么既然有保存了,就必须有清除功能。 在Mac电脑中,如何对Git的用户名和密码进行修改呢?起初不懂Mac,所以整了很久,本文将记录如何对这个进行操作,以便后期使用。
在Mac电脑中,如何对Git的用户名和密码进行修改呢?起初不懂Mac,所以整了很久,本文将记录如何对这个进行操作,以便后期使用。 Docker编译镜像出现:fetch http://dl-cdn.alpinelinux.org/alpine/v3.12/main/x86_64/APKINDEX.tar.gz
ERROR: http://dl-cdn.alpinelinux.org/alpine/v3.12/main: temporary error (try again later)
WARNING: Ignoring APKINDEX.2c4ac24e.tar.gz: No such file or directory问题
Docker编译镜像出现:fetch http://dl-cdn.alpinelinux.org/alpine/v3.12/main/x86_64/APKINDEX.tar.gz
ERROR: http://dl-cdn.alpinelinux.org/alpine/v3.12/main: temporary error (try again later)
WARNING: Ignoring APKINDEX.2c4ac24e.tar.gz: No such file or directory问题