优先队列(Priority Queue)

xiaohai 2022-03-30 15:05:03 共2022人围观 标签： 算法 
简介普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删除。在优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。优先队列具有最高级先出 （first in, largest out）的行为特征。通常采用堆数据结构来实现。

4.10.1、优先队列定义

普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删除。在优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。优先队列具有最高级先出 （first in, largest out）的行为特征。通常采用堆数据结构来实现。

优先队列按照作用不同，分为：

  • 最大优先队列：可以获取并删除队列中最大的值
  • 最小优先队列：可以获取并删除队列中最小的值

4.10.2、最大优先队列

4.10.2.1、最大优先队列API设计

类名 MaxPriorityQueue
构造方法 MaxPriorityQueue(int capacity)：创建容量为capacity的MaxPriorityQueue对象
成员变量 private T[] items：用来存储元素数组
private int N：记录堆中的元素个数
成员方法 private boolean less(int i,int j)：判断堆中索引i处的元素是否小于索引j处的元素
private void exch(int i,int j)：交换索引i和索引j处的值
public T delMax()：删除堆中最大的元素，并返回这个最大值
private void swim(int k)：使用上浮算法，使索引k处的元素能在堆中处于一个正确的位置
private void sink(int k)：使用下沉算法，使索引k处的元素能在堆中处于一个正确的位置
public void insert(T t)：往堆中插入一个元素
public int size()：获取队列中元素个数
public boolean isEmpty()：判断队列是否为空

4.10.2.2、最大优先队列实现

实现类

package cn.test.algorithm.datastruct;

public class MaxPriorityQueue<T extends Comparable<T>> {
    //存储元素
    private T[] items;

    //元素个数
    private int N;

    public MaxPriorityQueue(int capacity) {
        this.items = (T[]) new Comparable[capacity + 1];
        this.N = 0;
    }

    //队列个数
    public int size() {
        return N;
    }

    public boolean isEmpty() {
        return N == 0;
    }

    //最小值
    private boolean less(int i, int j) {
        return items[i].compareTo(items[j]) < 0;
    }

    //交换值
    private void exch(int i, int j) {
        T tmp = items[i];
        items[i] = items[j];
        items[j] = tmp;
    }

    //插入
    public void insert(T t) {
        items[++N] = t;
        swim(N);
    }

    //删除最大值
    public T delMax() {
        if (N == 0) {
            return null;
        }
        T max = items[1];
        exch(1, N);
        items[N] = null;
        N--;
        sink(1);
        return max;
    }

    //上浮
    public void swim(int k) {
        while (k > 1) {
            if (less(k / 2, k)) {
                exch(k / 2, k);
            }
            k = k / 2;
        }
    }

    //下沉
    private void sink(int k) {
        while (2 * k < N) {
            int max = 2 * k;
            if (2 * k + 1 <= N) {
                if (less(2 * k, 2 * k + 1)) {
                    max = 2 * k + 1;
                }
            }

            if (!less(k, max)) {
                break;
            }

            exch(k, max);

            k = max;
        }
    }
}

测试类

package cn.test.algorithm.test;

import cn.test.algorithm.datastruct.MaxPriorityQueue;

public class MaxPriorityQueueTest {
    public static void main(String[] args) {
        MaxPriorityQueue<Integer> queue = new MaxPriorityQueue<Integer>(100);
        queue.insert(1);
        queue.insert(5);
        queue.insert(2);
        queue.insert(9);
        queue.insert(7);
        queue.insert(100);

        System.out.println("队列元素个数：" + queue.size());
        Integer result = null;
        while (true) {
            result = queue.delMax();
            if (result == null) {
                break;
            }
            System.out.println("依次删除队列中最大的元素:" + result);
        }

        System.out.println("队列是否为空:" + queue.isEmpty());
    }
}

测试结果

队列元素个数：6
依次删除队列中最大的元素:100
依次删除队列中最大的元素:9
依次删除队列中最大的元素:7
依次删除队列中最大的元素:5
依次删除队列中最大的元素:2
依次删除队列中最大的元素:1
队列是否为空:true

从上面可以看出优先队列其实就是跟堆的实现差不多，只不过是多了两个方法而已。

4.10.3、最小优先队列

特性：

  • 最小元素放在数组索引1处
  • 每个结点的数据总是小于或等于它的两个子节点

    4.10.3.1、最小优先队列API设计

类名 MinPriorityQueue
构造方法 MinPriorityQueue(int capacity)：创建容量为capacity的MinPriorityQueue对象
成员变量 private T[] items：用来存储元素数组
private int N：记录堆中的元素个数
成员方法 private boolean less(int i,int j)：判断堆中索引i处的元素是否小于索引j处的元素
private void exch(int i,int j)：交换索引i和索引j处的值
public T delMin()：删除堆中最小的元素，并返回这个最小值
private void swim(int k)：使用上浮算法，使索引k处的元素能在堆中处于一个正确的位置
private void sink(int k)：使用下沉算法，使索引k处的元素能在堆中处于一个正确的位置
public void insert(T t)：往堆中插入一个元素
public int size()：获取队列中元素个数
public boolean isEmpty()：判断队列是否为空

4.10.3.2、最小优先队列实现

实现类

package cn.test.algorithm.datastruct;

public class MinPriorityQueue<T extends Comparable<T>> {
    //存储元素
    private T[] items;

    //元素个数
    private int N;

    public MinPriorityQueue(int capacity) {
        this.items = (T[]) new Comparable[capacity + 1];
        this.N = 0;
    }

    //队列个数
    public int size() {
        return N;
    }

    public boolean isEmpty() {
        return N == 0;
    }

    //最小值
    private boolean less(int i, int j) {
        return items[i].compareTo(items[j]) < 0;
    }

    //交换值
    private void exch(int i, int j) {
        T tmp = items[i];
        items[i] = items[j];
        items[j] = tmp;
    }

    //插入
    public void insert(T t) {
        items[++N] = t;
        swim(N);
    }

    //删除最小值
    public T delMin() {
        if (N == 0) {
            return null;
        }
        T max = items[1];
        exch(1, N);
        items[N] = null;
        N--;
        sink(1);
        return max;
    }

    //上浮
    public void swim(int k) {
        while (k > 1) {
            if (less(k, k / 2)) {
                exch(k, k / 2);
            }
            k = k / 2;
        }
    }

    //下沉
    private void sink(int k) {
        while (2 * k <= N) {
            int min = 2 * k;
            if (2 * k + 1 <= N) {
                if (!less(2 * k, 2 * k + 1)) {
                    min = 2 * k + 1;
                }
            }

            if (less(k, min)) {
                break;
            }

            exch(k, min);

            k = min;
        }
    }
}

测试类

package cn.test.algorithm.test;

import cn.test.algorithm.datastruct.MinPriorityQueue;

public class MinPriorityQueueTest {
    public static void main(String[] args) {
        MinPriorityQueue<Integer> queue = new MinPriorityQueue<Integer>(100);
        queue.insert(1);
        queue.insert(5);
        queue.insert(2);
        queue.insert(9);
        queue.insert(7);
        queue.insert(100);

        System.out.println("队列元素个数：" + queue.size());
        Integer result = null;
        while (true) {
            result = queue.delMin();
            if (result == null) {
                break;
            }
            System.out.println("依次删除队列中最小的元素:" + result);
        }

        System.out.println("队列是否为空:" + queue.isEmpty());
    }
}

测试结果

队列元素个数：6
依次删除队列中最小的元素:1
依次删除队列中最小的元素:2
依次删除队列中最小的元素:5
依次删除队列中最小的元素:7
依次删除队列中最小的元素:9
依次删除队列中最小的元素:100
队列是否为空:true

最大优先队列采用的是最大堆，就是索引1处值是最大值；最小优先队列采用的是最小堆，就是索引1处值是最小值。

4.10.4、索引最小优先队列

在前面实现的最大和最小优先队列中，可以快速查找队列的中的最大值或最小值，但是有一个缺点就是没有办法通过索引访问以存在于队列中的对象，并更新他们。为了实现这个目录，就需要索引优先对队列。这里主要采用最小索引优先队列为例。

思路：就是需要两个辅助数组来存储堆数组的元素和索引的对应关系。

图片alt

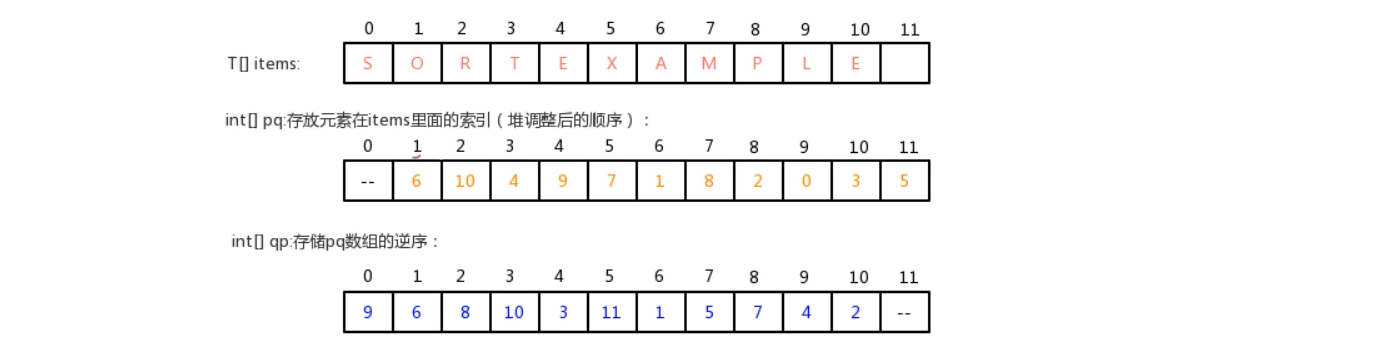
4.10.4.1、索引最小优先队列API设计

类名 IndexMinPriorityQueue
构造方法 IndexMinPriorityQueue(int capacity)：创建容量为capacity的IndexMinPriorityQueue对象
成员变量 private T[] items：用来存储元素数组
private int N：记录堆中的元素个数
private int[] pq：保存每个元素在item数组中的索引，pq数组需要堆有序
private int[] qp：保存pq的逆序，pq的值作为索引，pq的索引作为值
成员方法 private boolean less(int i,int j)：判断堆中索引i处的元素是否小于索引j处的元素
private void exch(int i,int j)：交换索引i和索引j处的值
public T delMin()：删除堆中最小的元素，并返回这个最小值
private void swim(int k)：使用上浮算法，使索引k处的元素能在堆中处于一个正确的位置
private void sink(int k)：使用下沉算法，使索引k处的元素能在堆中处于一个正确的位置
public void insert(int i,T t)：往堆中插入一个元素
public int size()：获取队列中元素个数
public boolean isEmpty()：判断队列是否为空
public boolean contains(int k):判断k对应的元素是否存在
public void changeItem(int i,T t):改变索引i处的元素值
public int minIndex()：最小元素关联的索引
public int delete(int i):删除索引i关联的元素

4.10.4.2、索引最小优先队列实现

实现类

package cn.test.algorithm.datastruct;

import java.util.Arrays;

public class IndexMinPriorityQueue<T extends Comparable<T>> {
    //存储元素
    private T[] items;

    //元素个数
    private int N;

    //保存每个元素在item数组中的索引，pq数组需要堆有序
    private int[] qp;

    //保存pq的逆序，pq的值作为索引，pq的索引作为值，方便查找
    private int[] pq;

    public IndexMinPriorityQueue(int capacity) {
        this.items = (T[]) new Comparable[capacity + 1];
        this.pq = new int[capacity + 1];
        this.qp = new int[capacity + 1];
        this.N = 0;
        //默认情况下，队列中没有任何数据，需要让qp和pq的元素都为-1
        for (int i = 0; i < qp.length; i++) {
            qp[i] = -1;
            pq[i] = -1;
        }
    }

    //队列个数
    public int size() {
        return N;
    }

    public boolean isEmpty() {
        return N == 0;
    }

    //最小值
    private boolean less(int i, int j) {
        return items[pq[i]].compareTo(items[pq[j]]) < 0;
    }

    //交换值
    private void exch(int i, int j) {
        //交换pq
        int tmp = pq[i];
        pq[i] = pq[j];
        pq[j] = tmp;

        //更新qp
        qp[pq[i]] = i;
        qp[pq[j]] = j;
    }

    //判断k对应的元素是否存在
    public boolean contains(int k) {
        return qp[k] != -1;
    }

    //最小索引
    public int minIndex() {
        return pq[1];
    }

    //插入
    public void insert(int i, T t) {
        if (contains(i)) {
            return;
        }

        //元素+1
        N++;

        //把数据存放到item中
        items[i] = t;

        //把i存储到qp数组中
        pq[N] = i;
        //通过qp来记录pq中的i
        qp[i] = N;

        //通过堆上浮调整堆顺序
        swim(N);
    }

    //删除最小值
    public T delMin() {
        if (N == 0) {
            return null;
        }

        //获取最小元素对应的索引
        int minIndex = minIndex();
        T min = items[minIndex];

        //交换pq中1处和最大索引处的元素
        exch(1, N);

        //删除qp中对应的内容
        qp[pq[N]] = -1;

        //删除pq最大索引处的内容
        pq[N] = -1;

        //删除items中的元素
        items[minIndex] = null;

        //元素-1
        N--;

        //下沉调整
        sink(1);

        return min;
    }

    //删除指定位置内容
    public void delete(int i) {
        //找到i在pq中的索引
        int k = qp[i];

        //交换pq中索引k处值和索引N处的值
        exch(k, N);

        //删除qp中的内容
        qp[qp[N]] = -1;

        //删除items中的内容
        pq[N] = -1;

        //删除items中内容
        items[k] = null;

        //元素个数-1
        N--;
        //堆调整
        sink(k);
        swim(k);
    }

    //修改索引i处的值
    public void changeItem(int i, T t) {
        //修改items中i位置的元素
        items[i] = t;

        //找到i位置在pq中出现的位置
        int k = qp[i];

        //调整堆
        sink(k);
        swim(k);
    }

    //上浮
    public void swim(int k) {
        while (k > 1) {
            if (less(k, k / 2)) {
                exch(k, k / 2);
            }
            k = k / 2;
        }
    }

    //下沉
    private void sink(int k) {
        while (2 * k <= N) {
            int min = 2 * k;
            if (2 * k + 1 <= N) {
                if (!less(2 * k, 2 * k + 1)) {
                    min = 2 * k + 1;
                }
            }

            if (less(k, min)) {
                break;
            }

            exch(k, min);

            k = min;
        }
    }
}

测试类

package cn.test.algorithm.test;

import cn.test.algorithm.datastruct.IndexMinPriorityQueue;

public class IndexMinPriorityQueueTest {
    public static void main(String[] args) {
        IndexMinPriorityQueue<Integer> queue = new IndexMinPriorityQueue<Integer>(10);
        queue.insert(1, 10);
        queue.insert(2, 1);
        queue.insert(3, 3);
        queue.insert(4, 5);
        queue.insert(5, 6);
        queue.insert(6, 20);
        queue.insert(7, 7);
        queue.insert(8, 0);

        System.out.println("队列元素个数：" + queue.size());
        Integer result = null;
        while (!queue.isEmpty()) {
            int min = queue.delMin();
            System.out.println("依次删除队列中最小的元素:" + min);
        }

        System.out.println("队列是否为空:" + queue.isEmpty());
    }
}

测试结果

队列元素个数：8
依次删除队列中最小的元素:0
依次删除队列中最小的元素:1
依次删除队列中最小的元素:3
依次删除队列中最小的元素:5
依次删除队列中最小的元素:6
依次删除队列中最小的元素:7
依次删除队列中最小的元素:10
依次删除队列中最小的元素:20
队列是否为空:true

相同类型文章

热门标签

每日一句

    学会忍受不公平，学会恪尽职责。

    ——林肯

今日排行

  • Electron页面跳转、浏览器打开链接和打开新窗口

    Electron页面跳转、浏览器打开链接和打开新窗口

  • Git保存和清除用户名、密码

    在使用Git的过程中，不想每次都输入用户名和密码去拉取代码，所以就需要保存这些信息，那么既然有保存了，就必须有清除功能。

  • 嗨！Tauri

    Tauri 是一个框架，用于为所有主要桌面平台构建小巧、快速的二进制文件。开发人员可以集成任何可编译为 HTML、JS 和 CSS 的前端框架，以构建他们的用户界面。应用程序的后端是一个基于 Rust 的二进制文件，带有一个前端可以与之交互的 API。 Tauri 应用程序的用户界面目前在 macOS 和 Windows 上利用 tao 作为窗口处理库，在 Linux 上通过 Tauri 团队孵化和维护的 WRY 利用 WebKit、Windows 上的 WebView2 和 Linux 上的 WebKitGTK 创建一个统一的系统 webview（和其他好东西，如菜单和任务栏）接口。

  • Python3之format

    Python的format使用应该是比较常见的，但是在Python3中，format的使用是怎么样的呢？本文主要记录就是Python3中的format的使用。

  • 费马点模型

    费马点是指到一个三角形三个顶点距离之和最小的点，称为三角形的费马点。

点击排行

友情链接