初中数学:平面直角坐标系中三角形面积求法
学习了平面直角坐标系,本文我们开始介绍在平面直角坐标系中的三角形面积的求法。在阅读本文内容前,希望大家先看看《初中数学:平面坐标系中的距离》这篇文章,必须要先掌握平面直角坐标系中两点间的距离。下面开始进入正题。
一、求三角形的面积
1. 有一边在坐标轴上的三角形
例1、如图,在平面直角坐标系中,三角形ABC的顶点坐标分别为A(-3,0),B(0,3),C(0,-1),求三角形ABC的面积.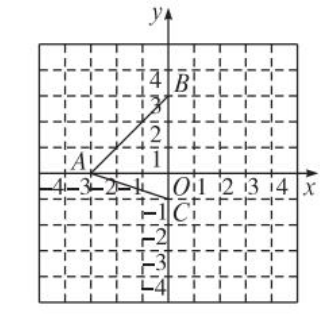
【分析】根据三个顶点的坐标可以看出,B、C两点都在y轴上,故直接可以得出BC的长度,A点到BC边的距离就是A点到y轴的距离,故A点的横坐标的绝对值3,然后根据三角形的面积公式求解即可。
解:∵ B(0,3),C(0,-1)
∴ BC=3-(-1)=4
∵ A(-3,0)
∴ A点到y轴的距离为AO=3
∴
2. 有一边与坐标轴平行的三角形
例2、如图,在平面直角坐标系中,已知点A(-1,5),B(-1,0),C(-4,3),求三角形ABC的面积.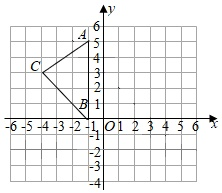
【分析】根据三个顶点坐标可以看出,A、B两点的横坐标相同,则AB平行于y轴,则AB的的距离为5,点C到AB的距离通过点C作AB的垂线,和容易得出点C到AB的距离为3,利用三角形面积公式求解即可。
解:∵ A(-1,5),B(-1,0)
∴ A、B两点的横坐标相同
∴ AB//y轴
∴ AB=5
∵ C(-4,3)
∴ C点到AB的距离为3
∴
3、三边均既不在坐标轴上也不平行于坐标轴
例3、如图,△AOB中,A,B两点的坐标分别为(2,4)、(6,2),求△AOB的面积.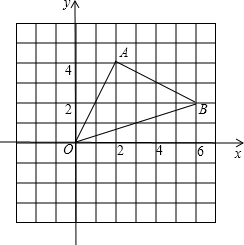
【分析】对于这种三边均既不在坐标轴上也不平行于坐标轴我们采用“割补法”来求三角形面积。
“补”:将三角形补成一个长方形或梯形,方法就是过三个顶点作坐标轴的平行线,先计算出长方形或梯形的面积,然后再减去多余的三角形面积。
“割”:找到三角形某边的整数点坐标,将这个点与另外的一个点连接起来,刚好这个线段平行于坐标轴,则将这个三角形分成两个三角形,将两个三角形的面积相加即可求解。“割”也不一定只能分成两个,多个也可以,但是要便于计算。
解:方法一(补):
如图,过点A、B分别作x轴、y轴的垂线CE、CF交点为C,垂足分别为E、F,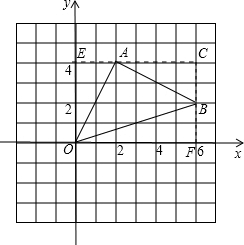
∵ A(2,4)、B(6,2)
∴ OE=AC=4,EA=CB=BF=2,OF=6,
∴S长方形ECFO=6×4=24
S△AOE=
S△ACB=
S△BOF=
∴S△AOB=SECFO-S△AOE-S△ACB-S△BOF
=24-4-4-6
=10
∴ △AOB的面积是10.
方法二(割):
如图:作BC//x轴交AC于点C,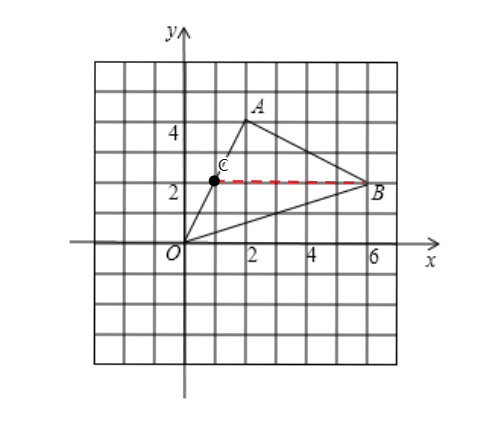
∴ 点C坐标为(1,2)
∵ B(6,2)
∴ BC=5
∴ S△ABC=
∴ S△ABO=S△ABC+S△OBC=5+5=10
注意:这样作辅助线是因为通过分析,刚好C点是整数点坐标,并且BC平行于x轴。如果过点A作y轴的平行线,则与OB相交的点不是整数点,就不能计算。
二、练习
1、如图,三角形ABC的三个顶点的坐标分别是A(4,0),B(-2,0),C(2,4),求三角形ABC的面积.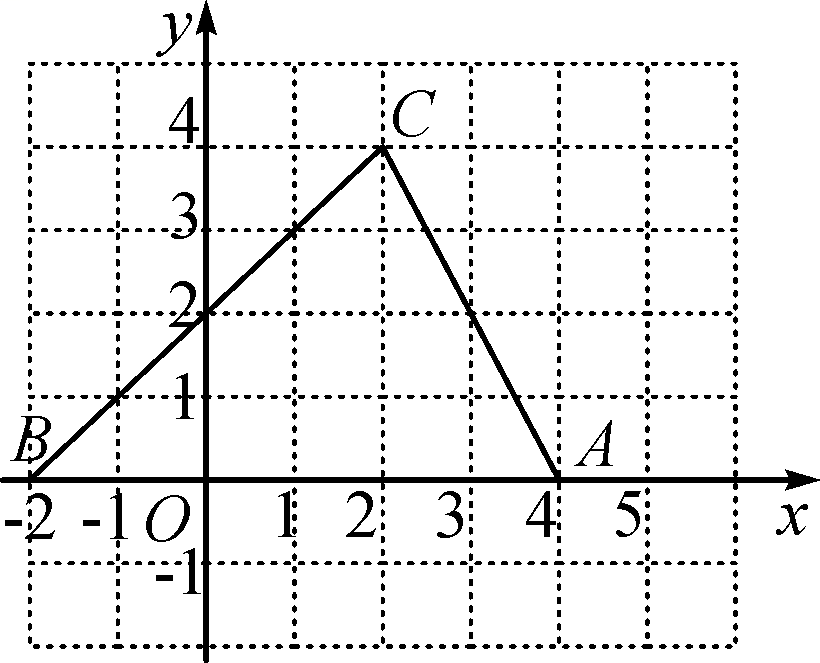
2、三角形ABC三个顶点的坐标分别为A(4,1),B(4,5),C(-1,2),求三角形ABC的面积.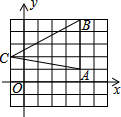
3、如图,平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(-3,-1),B(1,3),C(2,-3).求△ABC的面积.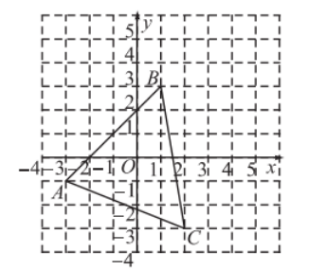
【答案】
1、解:∵A(4,0),B(-2,0),
∴ AB=4-(-2)=6.
∵C(2,4),
∴C点到x轴的距离,即AB边上的高为4,
∴
2、解:∵A,B两点的横坐标相同,
∴边AB∥y轴,∴AB=5-1=4.
作AB边上的高CD,则D点的横坐标为4,
∴CD=4-(-1)=5,
∴
3、解:如图,分别过B、C作y轴的垂线,再分别过A、C作x轴的垂线,组成矩形EFCR,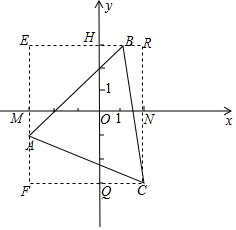
∵ A(-3,-1),B(1,3),C(2,-3)
∴ EH=FQ=3,EM=BN=3,FM=CN=3,RH=CQ=2,AM=1
∴ EM=3+1=4,BE=3+1=4,BR=2-1=1,RC=3+3=6,CF=2+3=5
∴ S△ABC=S矩形EFCR-S△BEA-S△AFC-S△BRC
=6×5-
=30-8-5-3
=14
在平面直角坐标系中求三角形的面积特别要注意三边既不平行于坐标轴也不在坐标轴上的三角形,一定要掌握好“割补法”,特别是“割”的用法,一定要注意。
 初中数学应熟记数值表(平方、立方、2的n次方、常用分数值)
初中数学应熟记数值表(平方、立方、2的n次方、常用分数值) 相似三角形是初中几何中非常重要的内容,常常与其他知识点结合,是中考的常考题型。本节主要介绍相似三角形模型——A字型和8字型模型
相似三角形是初中几何中非常重要的内容,常常与其他知识点结合,是中考的常考题型。本节主要介绍相似三角形模型——A字型和8字型模型 《是妈妈是女儿》聚焦母女间未曾言明的爱意,以书信对话的形式呈现出各自的内心独白,表达彼此的牵挂。黄绮珊与希林娜依·高用跨越时空、打开心扉、深情对唱的形式,将天下母女爱的寄语化作心灵的倾诉。黄绮珊的每一句话,每一个字都演绎出了妈妈对女儿的爱,而希林依娜·高把女儿对妈妈的爱由不理解到理解再到感恩演绎得淋漓尽致。
《是妈妈是女儿》聚焦母女间未曾言明的爱意,以书信对话的形式呈现出各自的内心独白,表达彼此的牵挂。黄绮珊与希林娜依·高用跨越时空、打开心扉、深情对唱的形式,将天下母女爱的寄语化作心灵的倾诉。黄绮珊的每一句话,每一个字都演绎出了妈妈对女儿的爱,而希林依娜·高把女儿对妈妈的爱由不理解到理解再到感恩演绎得淋漓尽致。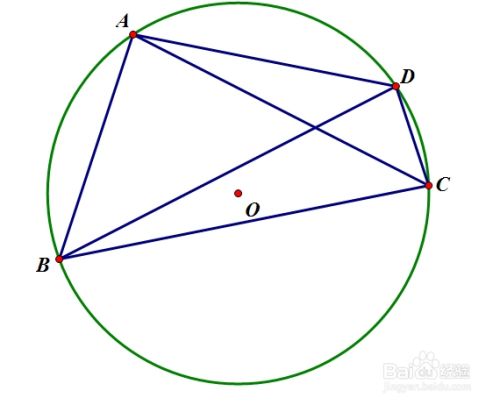 四点共圆:若在同一个平面内,有四个点在同一个圆上,则称这四个点共圆,一般简称“四点共圆”.
四点共圆:若在同一个平面内,有四个点在同一个圆上,则称这四个点共圆,一般简称“四点共圆”.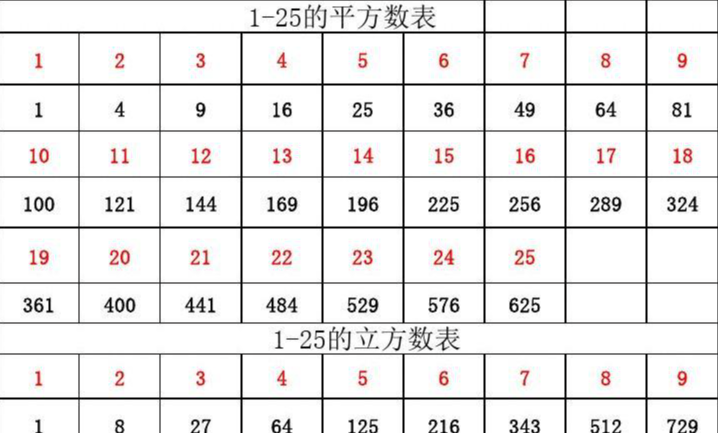 熟记常用数的平方和立方,对后期学习开平方和开立方奠定坚实的基础.
熟记常用数的平方和立方,对后期学习开平方和开立方奠定坚实的基础. 快速生成表格
快速生成表格 打包出现如下错误:Error: Application entry file "dist\electron\main.js" in the "D:\gui\demo2\build\win-unpacked\resources\app.asar" does not exist. Seems like a wrong configuration.
打包出现如下错误:Error: Application entry file "dist\electron\main.js" in the "D:\gui\demo2\build\win-unpacked\resources\app.asar" does not exist. Seems like a wrong configuration. Docker编译镜像出现:fetch http://dl-cdn.alpinelinux.org/alpine/v3.12/main/x86_64/APKINDEX.tar.gz
ERROR: http://dl-cdn.alpinelinux.org/alpine/v3.12/main: temporary error (try again later)
WARNING: Ignoring APKINDEX.2c4ac24e.tar.gz: No such file or directory问题
Docker编译镜像出现:fetch http://dl-cdn.alpinelinux.org/alpine/v3.12/main/x86_64/APKINDEX.tar.gz
ERROR: http://dl-cdn.alpinelinux.org/alpine/v3.12/main: temporary error (try again later)
WARNING: Ignoring APKINDEX.2c4ac24e.tar.gz: No such file or directory问题 在Mac电脑中,如何对Git的用户名和密码进行修改呢?起初不懂Mac,所以整了很久,本文将记录如何对这个进行操作,以便后期使用。
在Mac电脑中,如何对Git的用户名和密码进行修改呢?起初不懂Mac,所以整了很久,本文将记录如何对这个进行操作,以便后期使用。 在使用Git的过程中,不想每次都输入用户名和密码去拉取代码,所以就需要保存这些信息,那么既然有保存了,就必须有清除功能。
在使用Git的过程中,不想每次都输入用户名和密码去拉取代码,所以就需要保存这些信息,那么既然有保存了,就必须有清除功能。