等腰三角形存在性问题是中考的频繁考点，那么中考如考呢？
1、求满足情况的动点个数（客观题）；
2、求满足情况的动点坐标（解答题）。
本文主要介绍使用几何法解决等腰三角形的存在性问题.

一、引入问题

在平面内有一线段AB，点C为平面内任意一点，若△ABC为等腰三角形，则这样的点C有几个？点C的轨迹又是什么？

二、分析问题

根据等腰三角形的定义，要画等腰三角形，就必须知道以哪条边为底边。该问题只是给出了线段AB，C是平面内任意一点，所以就需要进行分类讨论，大致分AB是底边或AB是腰的两种情况。

三、解决问题

1、当AB是底边时，AC=BC，如图：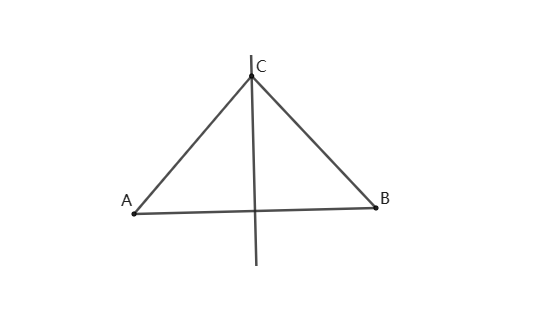

此时点C到点A和点B的距离相等，根据中垂线性质可知，点C只要在线段AB的垂直平分线上即可，但是要构成三角形，所以点C不能是AB中垂线与AB的交点处。
结论：点C有无数个，轨迹线段AB的中垂线（不含与AB的交点）

2、当AB为腰时，此时需要分两种情况
（1）当AB=AC时，如图：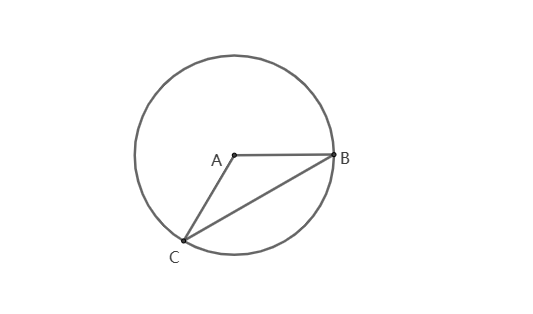

此时点A到点C和到点B的距离相等，那么点C是在以A点为圆心，AB为半径的圆上，但是要构成三角形，所以C点不能再B点和与A、B共线的点上。
结论：点C有无数个，轨迹是以点A为圆心，AB为半径的圆上（不含B点和与A、B的共线点）.
（2）当AB=BC时，如图：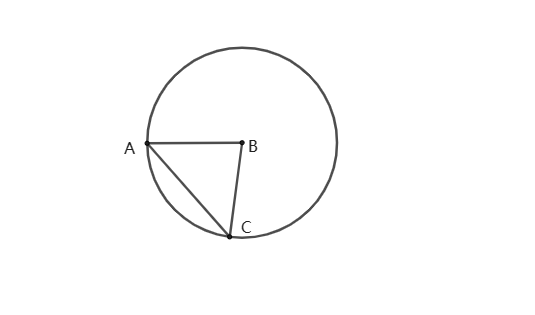

此时点B到点A和到点C的距离相等，那么点C是在以B点为圆心，AB为半径的圆上，但是要构成三角形，所以C点不能再A点和与A、B共线的点上。
结论：点C有无数个，轨迹是以点B为圆心，AB为半径的圆上（不含A点和与A、B的共线点）.

把三种情况放在同一图形中，如图：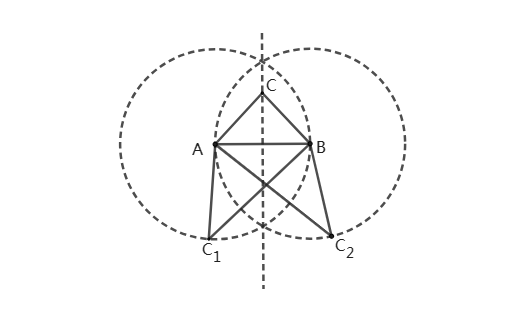

综上所述：点C有无数个，轨迹为一条直线和两个圆，称为“两圆一线”或“两圆一中垂”。

四、例题

1、如图所示，平面直角坐标系中有一点A(3,4)，在x轴上找一点P使得三角形OAP为等腰三角形。
解：（1）当AO=PO时，以点O为圆心，OA为半径作圆，如图：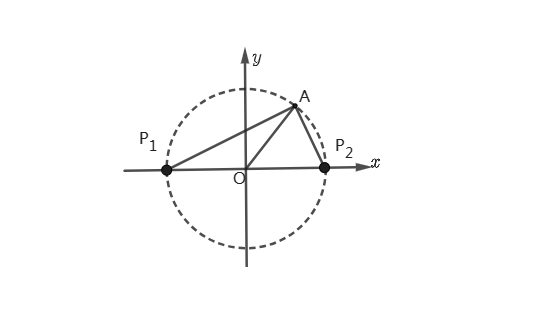

∵ OA=5
∴ OP=5
P_1(-5,0)，P_2(5,0)
（2）当AO=AP时，以点A为圆心，AO为半径作圆，如图：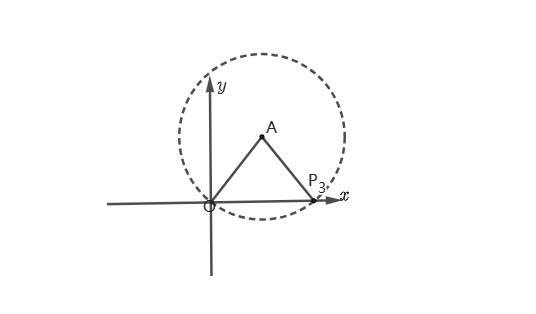

∵ OA=OP
∴ OP=6
P_3(6,0)
（3）当以OA边为底边，作OA的中垂线，如图：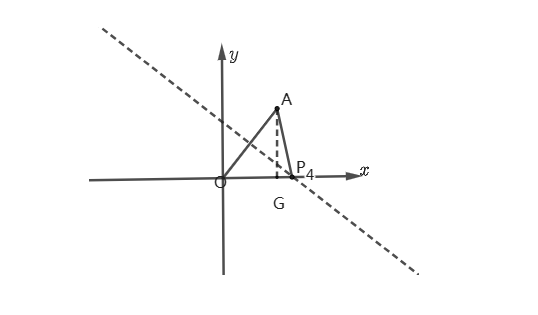

过点A作x轴的垂线，交x轴于点G
设AP=AP=a，则：GP=a-3
在Rt△AGP中
AG^3+GP^2=AP^2
∴ 4^2+(a-3)^2=a^2
解得：a=\frac{25}{6}
P_4(\frac{25}{6}，0)
综上所述，满足P点的坐标为（-5,0），（5,0），（6,0），(\frac{25}{6}，0).

2、如图，已知抛物线解析式为y=-x^2+2x+3，与x轴交于A、B两点，与y轴交于点C。在抛物线对称轴上是否存在一点P，使得△PCB为等腰三角形？若存在，请求出符合条件的P点坐标；若不存在说明理由？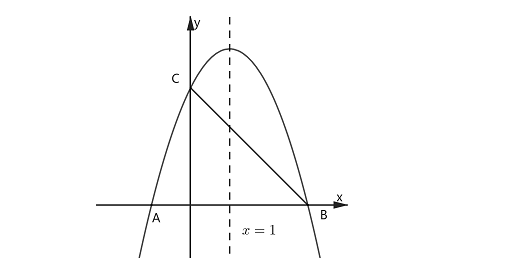

【分析】
1、如下图，以点B为圆心，BC长为半径作圆，圆与对称轴有两个交点，这两个点分别与B,C会构成等腰三角形，此时有PB=CB；
2、如下图，以点C为圆心，BC长为半径作圆，圆与对称轴有两个交点，这两个点分别与B,C会构成等腰三角形，此时有PC=BC；
3、如下图，作线段BC的中垂线和对称轴又会交于一点，这个点和B,C会构成等腰三角形，此时有PC=PB.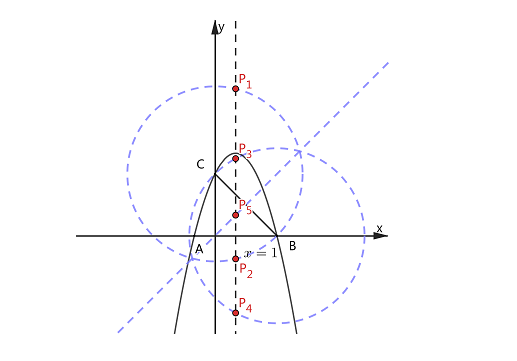

点P_1,P_2,P_3,P_4,P_5即为所求的5个点。既然点找到了，后面就是计算，可以自己先自己计算，本题的计算过程在后续文章中，请留心关注。

五、方法总结

1、找两定点并连接两定点，作两圆一线模型；
(以两定点为圆心，以定长为半径画圆，作定长线段的垂直平分线确定动点位置)
2、找两圆一线与动点运动轨迹的交点；
3、观察是否能直接得到动点的坐标，如不能直接看出就利用等腰三角形腰相等列关系，求坐标.