要计算算法的时间耗费情况,首先我们需要度量算法的执行时间,那么如何进行度量,本节我们将进行学习。
2.1.1、分析估算法
2.1.1.1、事后分析估算方法
比较容易想到的方法就是我们把算法的执行若干次,然后用计时器进行计时,这种是事后统计的方法看上不错。但是这种统计方法主要是通过设计好的测试程序和测试数据,利于用计算机计时器对不同的算法的程序的运行时间进行比较,从而确定算法效率的高低,就存在很大一个缺陷:必须依据算法实现编制好的测试程序,通常要花费大量的时间和精力,测试完了如果发现测试的非常糟糕,那么之前的所作的工作都白费了,并且在不同的测试环境,结果差异会很大。
public static void main(String[] args){
long start = System.currentTimeMillis();
int sum = 0;
int n = 100;
for(int i = 1;i <= n; i++){
sum += i;
}
System.out.println("sum=" + sum);
long end = System.currentTimeMillis();
System.out.println(end-start);
}
2.1.1.2、事前分析估算方法
在编写程序之前,依据统计方法对算法进行估算,经过总结,发现一个高级语言编写程序在计算机上运行所消耗的时间却决于下列因素:
- 算法采用的策略和方案
- 编译产生的代码质量
- 问题的输入规模
- 机器执行质量的速度
由此可见,抛开这些与计算机硬件、软件有关的因素,一个程序的运行时间依赖于算法的好坏和问题的输入规模。如果算法固定,那么该算法的执行时间就只和问题的输入规模有关系了。
需求1
计算1到100的和
第一种解法:
public static void main(String[] args){
int sum = 0;//执行1次
int n = 100;//执行1次
for(int i = 1; i <= n; i++){//执行n+1次
sum += i;//执行n次
}
System.out.println("sum = "+ sum);
}
如果n为1,需要计算1次,如果n为1亿,需要计算1亿次
第二种解法:
public static void main(String[] args){
int sum = 0;//执行1次
int n = 100;//执行1次
sum = (1 + n) * n / 2;//执行1次
System.out.println("sum = "+ sum);
}
如果n为1,需要计算1次,n为1亿,需要计算1次。
因此,当输入规模为n时,第一种算法总共执行了:1+1+n+1+n=2n+3次,第二种算法执行了:1+1+1=3次。如果我们把第一种算法的循环体看作时一个整体,忽略条件的判断,那么这这两种算法的运行时间差距就是n和1次的差距。
为什么循环判断在第一种算法里执行了n+1次,看起来是一个不小的数量,但是却可以忽略呢?下面再看一个例子:
需求2
计算100个1+100个2+100个3+…100个100的结果
public static void main(String[] args){
int sum = 0;
int n = 100;
for (int i = 1;i <= n; i++){
for(int j = 1; j <= n; j++){
sum += i;
}
}
System.out.println("sum="+sum);
}
在上面的例子中,如果我们要精确的研究循环的条件执行次数,是很麻烦的,并且真正计算和代码的是内循环的循环体,所以在研究算法的效率时,我们只需要考虑核心代码的执行次数,这样就可以简化。
研究算法复杂度侧重的是当输入规模不断增大时,算法的增长量的一个规律,而不是精确的定位需要执行多少次。
我们不关心编写程序的语言是什么,也不关系这些程序在什么计算机上运行,我们只关心它所实现的算法。这样不计算哪些循环索引的递增和循环终止的条件、变量声明、打印结果等操作,最终在分析程序的运行时间时,最重要的是把程序看作时独立于程序设计语言的算法或一系列步骤,我们分析一个算法的运行时间,最重要的就是把核心操作的次数和输入规模关联起来。
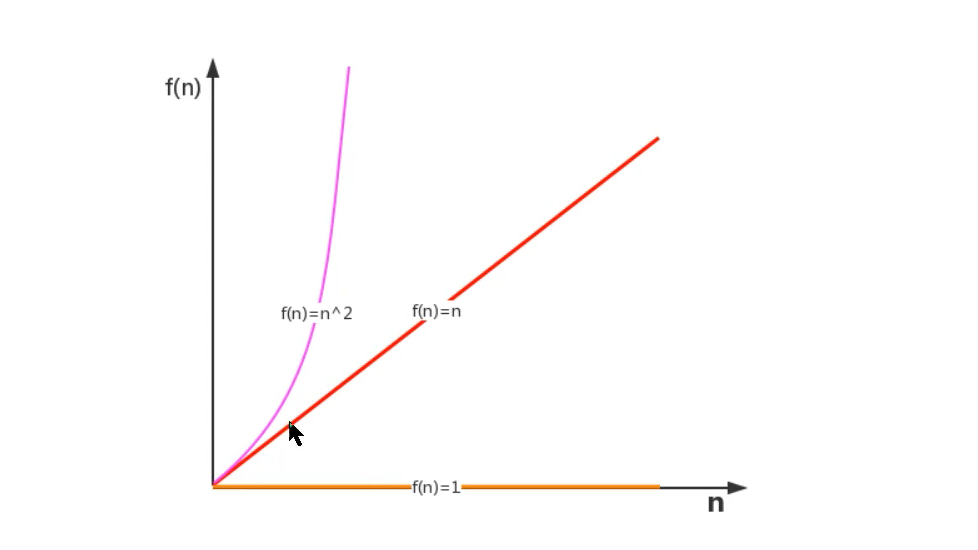
2.1.2、函数渐进增长
- 概念:给定两个函数f(n)和g(n),如果存在一个整数N,是的对于所有的n>N,f(n)总是比g(n)大,那么我们说f(n)的增长渐进快于g(n)。
概念不是很容易理解,下面我们做几个测试:
测试一
假设四个算法的输入规模都是n:
- 算法A1要做2n+3次操作
- 算法A2要做2n次操作
- 算法B1要做3n+1次操作
- 算法B2要做3n次操作
那么上述算法哪个更快一点呢?
| 输入规模 | 算法A1(2n+3) | 算法A2(2n) | 算法B1(3n+1) | 算法B2(3n) |
|---|---|---|---|---|
| n=1 | 5 | 2 | 4 | 3 |
| n=2 | 7 | 4 | 7 | 6 |
| n=3 | 9 | 6 | 10 | 9 |
| n=10 | 23 | 20 | 31 | 30 |
| n=100 | 203 | 200 | 301 | 300 |
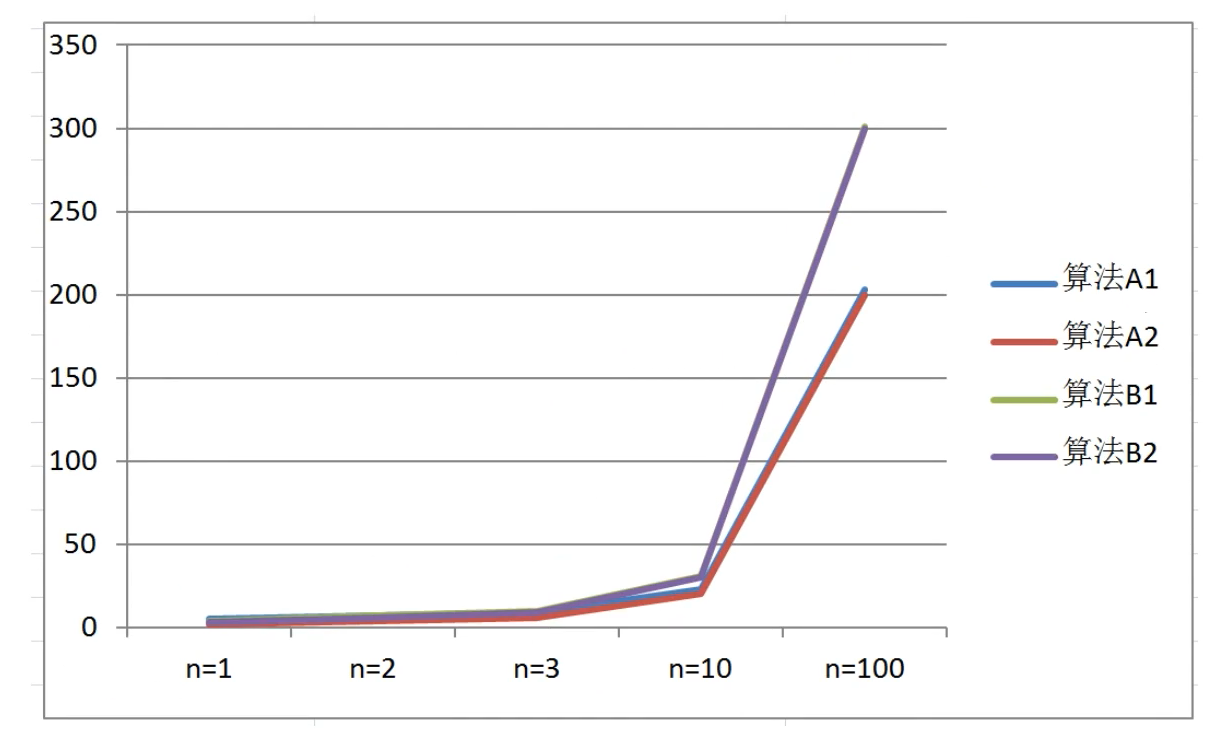
通过数据表格,比较算法A1和B1:
- 当输入规模n=1,A1的效率比B1的效率低
- 当输入规模n=2,A1的效率和B1的效率一样
- 当输入规模n>2,A1需要的执行次数一直都比B1的执行次数邵,所以A1效率比B1效率高
所以可以得出结论:
当输入规模n>2时,算法A1的渐进增长小于算法B1的渐进增长
通过观察折线图可以发现,随着输入规模的增大,算法A1和算法A2逐渐重叠在一块了,算法B1和算法B2也逐渐重叠在一起了,所以可以得出结论:
随着输入规模的增大,算法的常数项操作可以忽略不计
测试二
假设四个算法的输入规模都是n:
- 算法C1需要操作4n+8次
- 算法C2需要操作n次
- 算法D1需要操作2n^2+1次
- 算法D2需要操作n^2次
那么上述算法哪个更快一点呢?
| 输入规模 | 算法C1(4n+8) | 算法C2(n) | 算法D1(2n^2+1) | 算法D2(n^2) |
|---|---|---|---|---|
| n=1 | 12 | 1 | 3 | 1 |
| n=2 | 16 | 2 | 9 | 4 |
| n=3 | 20 | 3 | 19 | 9 |
| n=10 | 48 | 10 | 201 | 100 |
| n=100 | 408 | 100 | 20001 | 10000 |
| n=1000 | 4008 | 1000 | 2000001 | 1000000 |
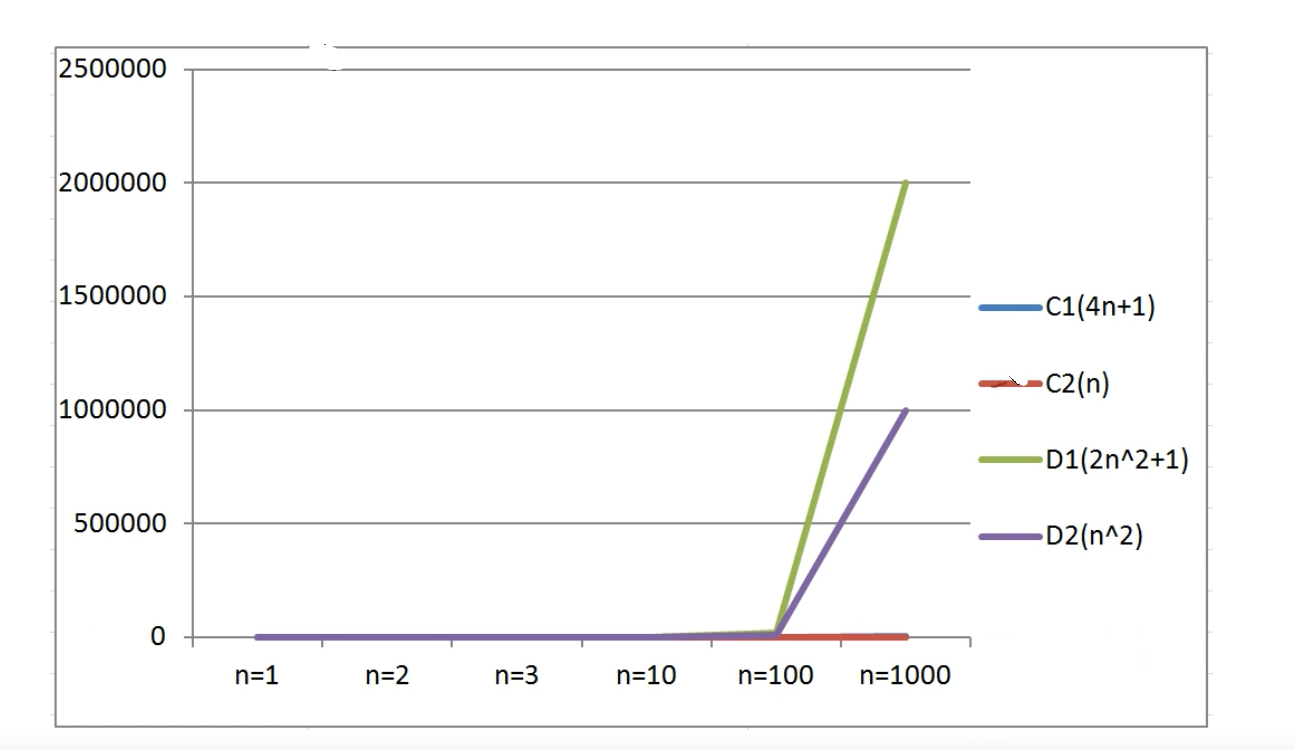
通过数据表格,对比算法C1和D1:
- 当输入规模n<=3时,算法C1执行次数多余算法D1,算法C1效果要低一些
- 当输入规模n>3时,算法C1执行次数少于算法D1,算法D1效率要低一些
所以总体来说C1要优于D1
通过折线图对比:
- 随着输入规模的增大,C1和C2几乎冲抵
- 随着输入规模的增大,去除n^2前面的常数因子,D系列的算法执行次数远远高于C系列
因此可以得出结论:
随着输入规模的增大,与最高次项相乘的常熟可以忽略
测试三
假设四个算法的输入规模都是n:
- 算法E1:2n^2+3n+1
- 算法E2:n^2
- 算法F1:2n^3+3n+1
- 算法F2:n^3
那么上述算法哪个更快一点呢?
| 输入规模 | 算法E1(2n^2+3n+1) | 算法E2(n^2) | 算法F1(2n^3+3n+1) | 算法D2(n^3) |
|---|---|---|---|---|
| n=1 | 6 | 1 | 6 | 1 |
| n=2 | 15 | 4 | 23 | 8 |
| n=3 | 28 | 9 | 64 | 27 |
| n=10 | 231 | 100 | 2031 | 1000 |
| n=100 | 20301 | 10000 | 2000301 | 1000000 |
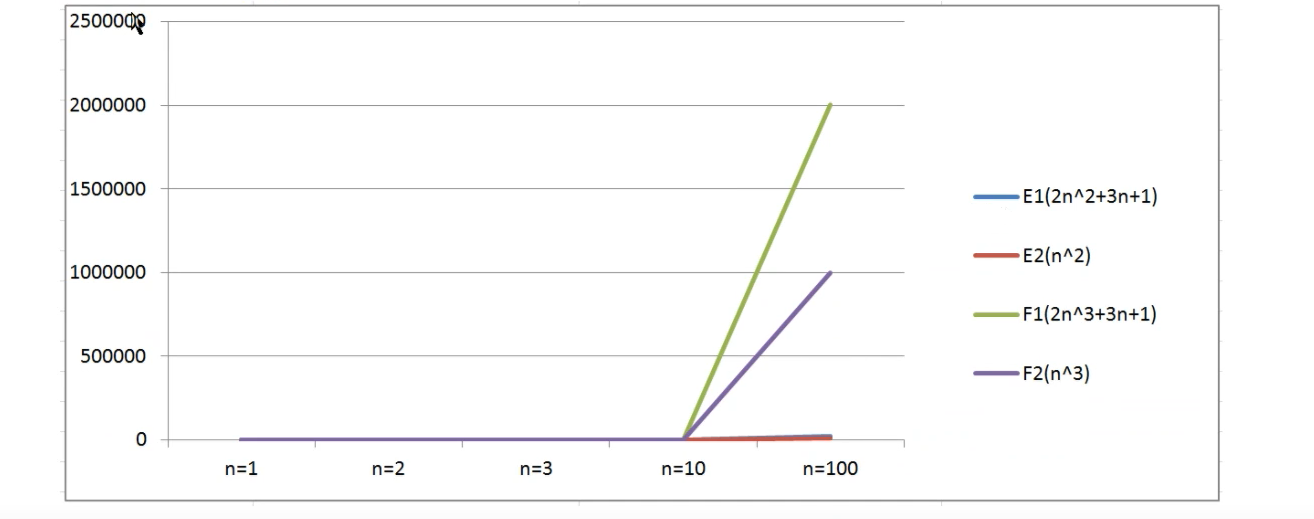
通过表格数据对比算法E1和F1:
- 当n=1时,算法E1和算法F1执行的次数是一样的
- 当n>1时,算法E1执行次数远远小于算法F1的执行次数
所以总体来说E1总体上优于算法F1
通过折线图可以看到,算法F系列随着n的增长变得特别快,算法E系列随着n的增长相比较算法F来说,变得比较慢,所以得出结论:
最高次项的指数越大,随着n的增长,结果也会变得增长特别快
测试四
假设五个算法的输入规模都是n:
- 算法G:n^3
- 算法H:n^2
- 算法I:n
- 算法J:log(n)
- 算法K:1
| 输入规模 | 算法G(n^3) | 算法H(n^2) | 算法I(n) | 算法J(log(n)) | 算法K(1) |
|---|---|---|---|---|---|
| n=2 | 8 | 4 | 2 | 1 | 1 |
| n=4 | 64 | 16 | 4 | 2 | 1 |
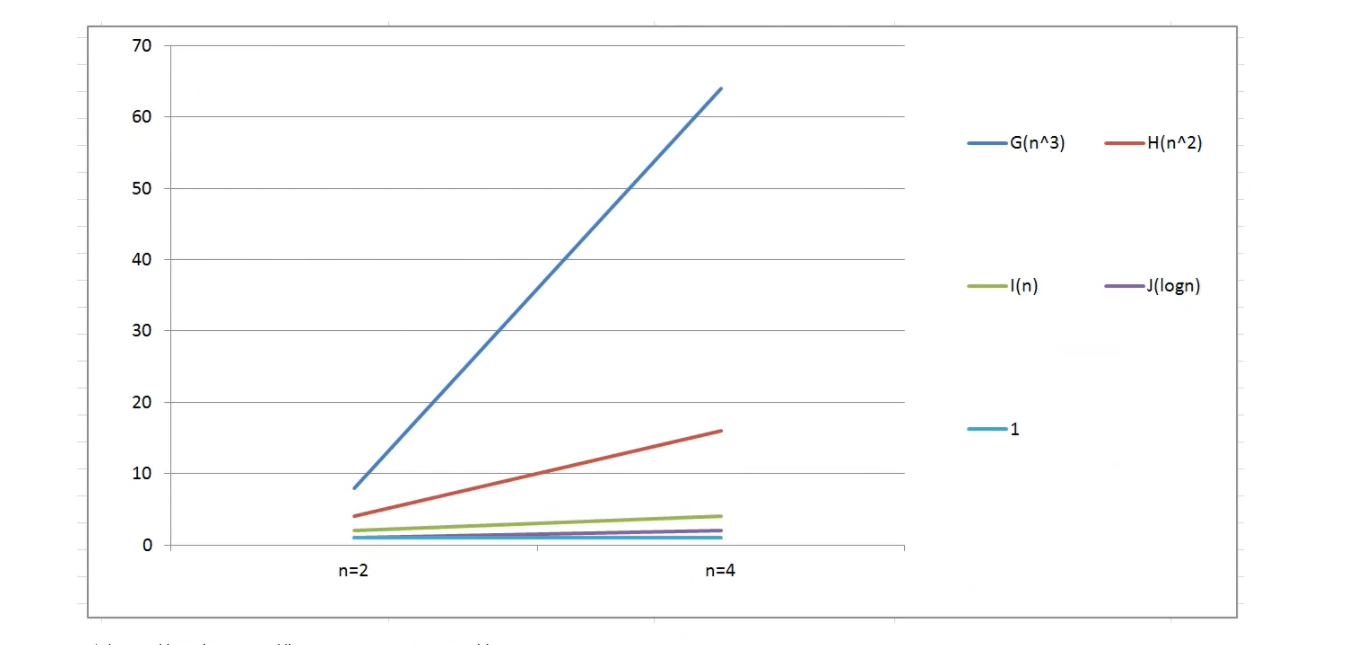
通过观察数据表和折线图可以得出结论:
算法函数中n的最高次幂越小,算法效率越高
综上所述,在我们比较算法输入规模的增长量时,可以有如下规则:
- 算法函数中的常数可以忽略
- 算法函数中的最高次幂的常数因子可以忽略
- 算法函数中的最高次幂越小,算法效率越高
2.1.3、算法时间复杂度
2.1.3.1、大O记法
- 定义:在进行算法分析时,语句总的执行次数T(n)时关于问题规模n的函数,进而分析T(n)随着n的变化情况而确定T(n)的量级。算法的时间复杂度,就是算法的时间度量,记作:T(n)=O(f(n))。它随着问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐进时间复杂读,简称时间复杂度,其中f(n)时问题规模n的某个函数。
在这里需要明确,执行次数=执行时间
用大写O来体现算法时间复杂度的记法,我们称为大O记法。一班情况下,随着输入规模n的增大,T(n)增长最慢的算法为最优算法。
下面使用大O表示法来表示一些求和算法的时间复杂度:
算法一:
public static void main(String[] args){
int sum = 0;//执行1次
int n = 100;//执行1次
sum = (1 + n) * n / 2;//执行1次
System.out.println("sum = "+ sum);
}
算法二:
public static void main(String[] args){
int sum = 0;//执行1次
int n = 100;//执行1次
for(int i = 1; i <= n; i++){//执行n+1次
sum += i;//执行n次
}
System.out.println("sum = "+ sum);
}
算法三:
public static void main(String[] args){
int sum = 0;//执行1次
int n = 100;//执行1次
for (int i = 1;i <= n; i++){
for(int j = 1; j <= n; j++){
sum += i;//执行2^n
}
}
System.out.println("sum="+sum);
}
以上执行次数各为:
- 算法一:3次
- 算法二:n+2次
- 算法三:n^2+2次
如果用大O记法表示上述的每个算法的时间复杂度,应该如何表示?基于前面学习的函数渐进增长的分析,推到大O阶的表示法有以下几个规则可以使用:
- 用常数1取代运行时间中的所有加法常数
- 在修改后的运算次数中,只保留最高阶项
- 如果最高阶项存在,且常数因子不为1,则去除与这个项相乘的常数
所以,上述算法的大O记法分别为:
- 算法一:O(1)
- 算法二:O(n)
- 算法三:O(n^2)
2.1.3.2、常见的大O阶
线性阶
一般含有非嵌套循环设计的线性阶,线性阶就是随着输入规模的增大,对应的计算次数也呈直线增长,例如:
public static void main(String[] args){
int sum = 0;//执行1次
int n = 100;//执行1次
for(int i = 1; i <= n; i++){//执行n+1次
sum += i;//执行n次
}
System.out.println("sum = "+ sum);
}
上面的代码,它的循环时间复杂度O(n),因为循环体中的代码需要执行n次。
平方阶
一般嵌套循环属于这种时间复杂度
public static void main(String[] args){
int sum = 0;//执行1次
int n = 100;//执行1次
for (int i = 1;i <= n; i++){
for(int j = 1; j <= n; j++){
sum += i;//执行2^n
}
}
System.out.println("sum="+sum);
}
上面的代码,n=100,也就是外层循环每执行一次,内层循环就执行100次,那总程序要循环出来就需要执行100*100次,就是n的平方,所以时间复杂度为O(n^2)
n方阶
一般多层嵌套循环属于中时间复杂度
public static void main(String[] args){
int sum = 0;//执行1次
int n = 100;//执行1次
for (int i = 1;i <= n; i++){
for(int j = 1; j <= n; j++){
//... 这里循环共循环了m次
sum += i;//执行2^n
}
}
System.out.println("sum="+sum);
}
上面的代码,n=100,也就是外层循环每执行一次,内层循环就执行100次,那总程序要循环出来就需要执行100100…*100次,就是n的m次方,所以时间复杂度为O(n^m)
对数阶
public static void main(String[] args){
int i=1,n=100;
while(i < n){
i = i * 2;
}
}
由于每次i*2之后,就距离n更近了一步,假设x个2相乘就退出循环,所以2^x=n,得到x=log(2),所以时间复杂度为:O(log(n))
对于对数阶,由于输入规模n的增大,不管底数为多少,他们增长趋势都是一样的,所以我们会忽略底数。
| 输入规模 | log(2)n | log(4)n | log(8)n |
|---|---|---|---|
| n=8 | 3 | 1.5 | 1 |
| n=64 | 6 | 3 | 2 |
| n=512 | 9 | 4.5 | 3 |
| n=4096 | 12 | 6 | 4 |
| n=16777216 | 24 | 12 | 8 |
| n=134217728 | 27 | 13.5 | 9 |
| n=2.815E+14 | 48 | 24 | 16 |
| n=7.923E+28 | 96 | 48 | 32 |
| n=6.28E+57 | 192 | 96 | 64 |
| n=3.94E+115 | 384 | 192 | 128 |
| n=1.55E+231 | 768 | 384 | 256 |
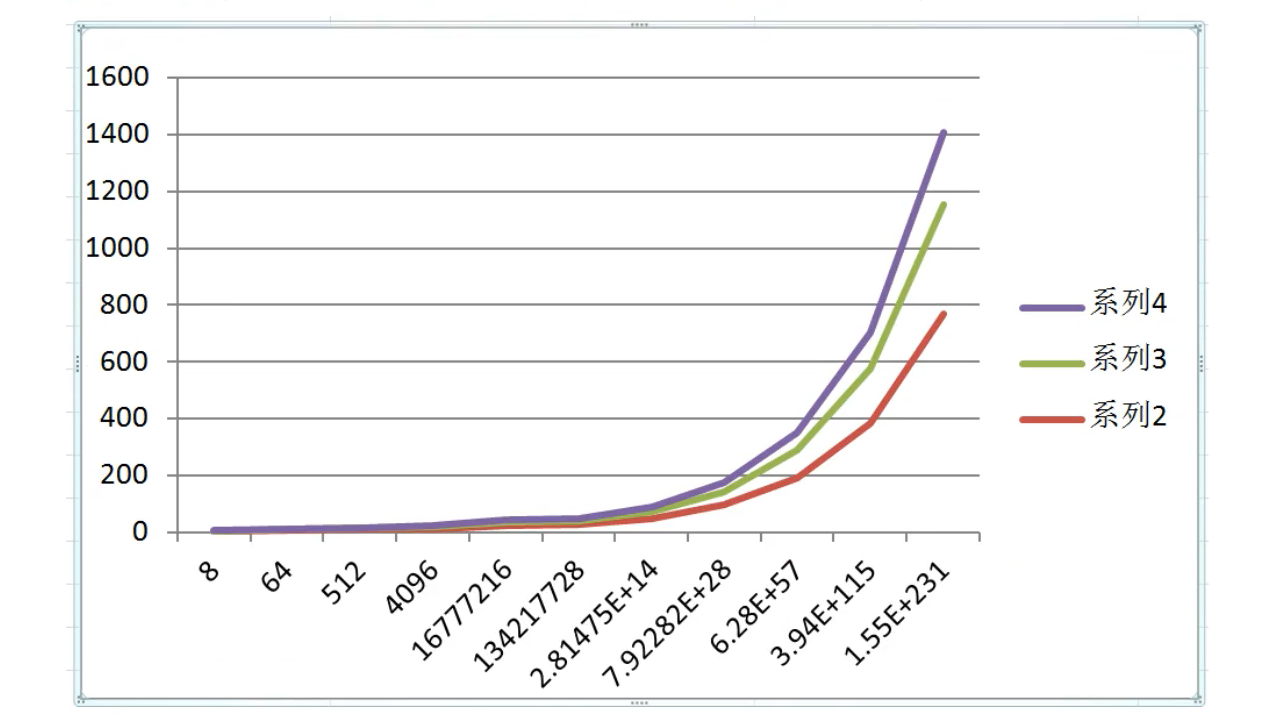
常数阶
一般不设计循环操作的都是常数阶,因为它不会随着n的增长而增长,如
public static void main(String[] args){
int sum = 0;//执行1次
int n = 100;//执行1次
sum = (1 + n) * n / 2;//执行1次
System.out.println("sum = "+ sum);
}
上面的代码不管输入规模n为多大,都是执行3次,所以时间复杂度就是O(1)
下面对常见的时间复杂度进行总结:
| 描述 | 增长的数量级 | 说明 | 例子 |
|---|---|---|---|
| 常数级别 | 1 | 普通语句 | 将两个数相加 |
| 对数级别 | logN | 二分策略 | 二分查找 |
| 线性级别 | N | 循环 | 找出最大元素 |
| 线性对数级别 | NlogN | 分治思想 | 归并排序 |
| 平方级别 | N^2 | 双层循环 | 检查所有元素对 |
| 立方级别 | N^2 | 三层循环 | 检查所有三元组 |
| 指数级别 | 2^N | 穷举查找 | 检查所有子集 |
他们的复杂度从低到高依次为:
O(1) < O(logN) < O(N) < O(NlogN) < O(n^2) < O(n^3)
所有我们尽可能的追求得是O(1)、O(logN)、O(N)、O(NlogN)这几种复杂度,如果发现时间复杂度有平方阶、立方阶或更复杂的,这种算法就是不合理的,就需要进行优化。
2.1.3.3、函数调用的时间复杂度分析
之前我们都是在一个函数内,实际场景中是不可能的,所以我们需要分析函数调用过程的时间复杂度。
案例一
public static void main(String[] args){
int n = 100;
for(int i = 1; i<= n; i++){
show(i);
}
}
private static void show(int i){
System.out.println(i);
}
在main方法中,有一个for循环,循环体调用了show方法,由于show方法内部执行了一行代码,所以show方法的时间复杂度为O(1),但是main方法的时间复杂度为O(n);
案例二
public static void main(String[] args){
int n = 100;
for(int i = 1; i<= n; i++){
show(n);
}
}
private static void show(int n){
for(int j = 1; j <= n; j++){
System.out.println(j);
}
}
在main方法中,有个for循环,循环体调用了show方法,由于show方法内部也有一个for循环,所以show方法的的时间复杂度为O(n),所以main方法的时间复杂度为O(n^2)
案例三
public static void main(String[] args){
int n = 100;
show(n);
for(int i = 1; i<= n; i++){
show(n);
}
for(int i = 1; i<= n; i++){
for(int j = 1; j <= n; j++){
System.out.println(j);
}
}
}
private static void show(int n){
for(int j = 1; j <= n; j++){
System.out.println(j);
}
}
- show方法的时间复杂度为O(n)
- show(n)为调用n次
- 第一个for循环内部又调用了show(n),所以调用次数为n^2次
- 第二个for循环内部还嵌套了for循环,所以调用次数为n^2次
所以整个main函数的内部调用次数为:n+n^2+n^2=2n^2+n,根据大O推导规则,去掉n保留最高项,去掉最高项的常数项2,所以main的时间复杂度为O(n^2)