链表是一种物理存储单元上非连续、非顺序的存储结构,其物理结构不能只管表示数据元素的逻辑顺序,数据元素的逻辑顺序是通过链表中的指针链接次序而实现的,链表由一系列的节点(链表中的每一个元素称为结点)组成,节点可以在运行时动态生成。
链表是解决顺序表中插入和删除元素出现大量数据移动情况。
4.3.1、结点API设计和实现
API设计
| 类名 | Node |
|---|---|
| 构造方法 | Node(T t,Node next):创建对象 |
| 成员变量 | T item:存储数据 Node next:指向下一个结点 |
结点类实现
public class Node<T>{
public T item;
public Node next;
public Node(T item,Node next){
this.item = item;
this.next = next;
}
}
结点使用
public static void main(String[] args){
//生成结点
Node<Integer> one = new Node(1,null);
Node<Integer> two = new Node(2,null);
Node<Integer> three = new Node(3,null);
Node<Integer> four = new Node(4,null);
Node<Integer> five = new Node(5,null);
//生成链表
one.next = two;
tow.next = three;
three.next = four;
four.next = five;
}
4.3.2、单向链表
4.3.2.1、定义
单向链表是链表的一种,它由多个结点组成,每个结点都是一个数据域和一个指针域组成,数据域来存储数据,指针域用来指向下一个节点。链表的头结点的数据域不存储数据,指针域指向第一个真正存储数据的节点。

4.3.2.2、API设计和实现
API设计
| 类名 | LinkList |
|---|---|
| 构造方法 | LinkList():创建LinkList()对象 |
| 成员内部类 | private class Node |
| 成员变量 | private Node head:记录首结点 private int N:记录链表的长度 |
| 成员方法 | public void clear():清空线性表 public boolean isEmpty():判断线性表是否为空,是返回true,否返回false public int length():返回线性表的个数 public T get(int i):获取指定下标的元素 public void insert(int i,T t):指定位置插入元素 public void insert(T t):插入到线性表的最后 public T remove(int t):删除并返回线性表的第i个元素 public int indexOf(T t):返回线性表中首次出现指定数据元素的位置序号,若不存在,返回-1 |
实现类
package cn.test.algorithm.datastruct;
import java.util.Iterator;
public class LinkList<T> implements Iterable<T> {
@Override
public Iterator<T> iterator() {
return new LIterator();
}
private class LIterator implements Iterator {
private Node n;
public LIterator() {
this.n = head;
}
@Override
public boolean hasNext() {
return n.next != null;
}
@Override
public Object next() {
n = n.next;
return n.item;
}
}
//内部类
private class Node {
T item;//存储数据
Node next;//下一个结点
public Node(T item, Node next) {
this.item = item;
this.next = next;
}
}
private Node head;//记录头结点
private int N;//记录链表的长度
//构造方法
public LinkList() {
//初始化头结点
this.head = new Node(null, null);
//初始化元素个数
this.N = 0;
}
//清空链表
public void clear() {
//将头结点的指向设置为null
this.head.next = null;
//设置元素的个数为0
this.N = 0;
}
//获取链表长度
public int length() {
return N;
}
//判断链表是否为空
public boolean isEmpty() {
return N == 0;
}
//获取指定位置的元素
public T get(int i) {
//通过循环从头结点开始往后找
Node node = this.head;
for (int index = 0; index < i; index++) {
node = node.next;
}
return node.item;
}
//插入
public void insert(T t) {
Node node = this.head;
//找到当前链表的最后一个结点
for (int index = 0; index < N; index++) {
node = node.next;
}
//创建新结点,保存元素
Node newNode = new Node(t, null);
//让当前链表最后一个结点指向新结点
node.next = newNode;
//元素个数+1
N++;
}
//指定位置插入
public void insert(T t, int i) {
Node node = this.head;
//找到i位置前一个结点
for (int index = 0; index < i - 1; index++) {
node = node.next;
}
//找到i位置的节点
Node nodeI = node.next;
//创建一个新结点,并且需要指向原来i位置的节点
Node newNode = new Node(t, nodeI);
//原来i位置的前一个节点指向新结点即可
node.next = newNode;
//元素+1
N++;
}
//删除指定元素的位置
public T remove(int i) {
Node node = this.head;
//找到i位置的前一个节点
for (int index = 0; index < i - 1; index++) {
node = node.next;
}
//找到i位置的节点
Node nodeI = node.next;
//把i位置的下一个结点指向i位置的前一个节点
node.next = nodeI.next;
//元素-1
N--;
return nodeI.item;
}
//根据结点值获取第一次出现的位置
public int indexOf(T item) {
Node node = this.head;
int i = 1;
while (true) {
if (node == null || node.item.equals(item)) {
break;
}
node = node.next;
i++;
}
return i;
}
@Override
public String toString() {
return "LinkList{" +
"head=" + head +
", N=" + N +
'}';
}
}
测试类
package cn.test.algorithm.test;
import cn.test.algorithm.datastruct.LinkList;
public class TestLinkList {
public static void main(String[] args) {
LinkList<Integer> link = new LinkList<>();
link.insert(1);
link.insert(2);
link.insert(3);
link.insert(4);
System.out.println(link.toString());
for (Integer integer : link) {
System.out.println("遍历值:" + integer);
}
link.insert(5, 1);
System.out.println(link.toString());
for (Integer integer : link) {
System.out.println("遍历值:" + integer);
}
//删除第二个位置的元素
link.remove(2);
System.out.println(link.toString());
for (Integer integer : link) {
System.out.println("遍历值:" + integer);
}
//清空
link.clear();
System.out.println(link.toString());
for (Integer integer : link) {
System.out.println("遍历值:" + integer);
}
}
}
运行结果
LinkList{head=cn.test.algorithm.datastruct.LinkList$Node@4554617c, N=4}
遍历值:1
遍历值:2
遍历值:3
遍历值:4
LinkList{head=cn.test.algorithm.datastruct.LinkList$Node@4554617c, N=5}
遍历值:5
遍历值:1
遍历值:2
遍历值:3
遍历值:4
LinkList{head=cn.test.algorithm.datastruct.LinkList$Node@4554617c, N=4}
遍历值:5
遍历值:2
遍历值:3
遍历值:4
LinkList{head=cn.test.algorithm.datastruct.LinkList$Node@4554617c, N=0}
4.3.3、双向链表
4.3.3.1、定义
双向链表也叫双向表,是链表的一种,它由多个结点组成,每个结点都由一个数据域和两个指针域组成,数据域用来存放数据,其中一个指针域指向后继结点,另一个指针用来指向前驱结点。链表的头结点的数据域不存储数据,指向前驱结点的指针值为null,指向后续结点的指针域指向第一个真正的存储数据的节点。

4.3.3.2、双向链表结点API设计和实现
API设计
| 类名 | Node |
|---|---|
| 构造方法 | Node(T t,Node next):创建对象 |
| 成员变量 | T item:存储数据 Node next:指向下一个结点 Node pre:指向上一个结点 |
结点实现类
public class Node<T>{
public T item;
public Node pre;
public Node next;
public Node(T item,Node pre,Node next){
this.item = item;
this.pre = pre;
this.next = next;
}
}
4.3.3.3、双向链表API设计和实现
| 类名 | TwoWayLinkList |
|---|---|
| 构造方法 | TwoWayLinkList():创建TwoWayLinkList()对象 |
| 成员内部类 | private class Node |
| 成员变量 | private Node first:记录首结点 private Node last:记录尾结点 private int N:记录链表的长度 |
| 成员方法 | public void clear():清空线性表 public boolean isEmpty():判断线性表是否为空,是返回true,否返回false public int length():返回线性表的个数 public T get(int i):获取指定下标的元素 public void insert(int i,T t):指定位置插入元素 public void insert(T t):插入到线性表的最后 public T remove(int t):删除并返回线性表的第i个元素 public int indexOf(T t):返回线性表中首次出现指定数据元素的位置序号,若不存在,返回-1 public T getFirst():获取第一个元素 public T getLast():获取尾元素 |
实现类
package cn.test.algorithm.datastruct;
import java.util.Iterator;
public class TwoWayLinkList<T> implements Iterable<T> {
private Node first;//首结点
private Node last;//尾节点
private int N;//长度
@Override
public Iterator<T> iterator() {
return new TIterator();
}
private class TIterator implements Iterator {
private Node n;
public TIterator() {
this.n = first;
}
@Override
public boolean hasNext() {
return n.next != null;
}
@Override
public Object next() {
n = n.next;
return n.item;
}
}
//内部结点类
private class Node {
public T item;
public Node pre;
public Node next;
public Node(T item, Node pre, Node next) {
this.item = item;
this.pre = pre;
this.next = next;
}
}
//构造方法
public TwoWayLinkList() {
//初始化首节点和尾节点
this.first = new Node(null, null, null);
this.last = null;
//初始化元素个数
this.N = 0;
}
//清理
public void clear() {
//首节点回到初始化
this.first.pre = null;
this.first.next = null;
this.first.item = null;
//尾节点
this.last = null;
this.N = 0;
}
@Override
public String toString() {
return "TwoWayLinkList{" +
"first=" + first +
", last=" + last +
", N=" + N +
'}';
}
//获取长度
public int length() {
return this.N;
}
//是否为空
public boolean isEmpty() {
return this.N == 0;
}
//插入
public void insert(T t) {
//如果为空,说明首节点就是尾节点
if (isEmpty()) {
//生成新结点,前驱结点是first
Node newNode = new Node(t, first, null);
//新结点作为尾节点
last = newNode;
//首节点的后继结点指向last结点
first.next = last;
} else {
//生成新结点,前驱结点是last
Node newNode = new Node(t, last, null);
//当前的last结点的后继结点指向新结点
last.next = newNode;
//新的尾节点为
last = newNode;
}
//元素+1
N += 1;
}
//指定位置插入
public void insert(T t, int i) {
//找到i位置的前一个节点
Node pre = first;
for (int index = 0; index < i - 1; index++) {
pre = pre.next;
}
//找到i位子的节点
Node currentNode = pre.next;
//创建新结点
Node newNode = new Node(t, pre, currentNode);
//让i位置的前一个节点的的下一个结点变为新结点
pre.next = newNode;
//让i位置的前一个节点变为新结点
currentNode.pre = newNode;
//元素+1
N++;
}
//获取第i个位置元素
public T get(int i) {
Node node = first.next;
for (int index = 0; index < i; index++) {
node = node.next;
}
return node.item;
}
//获取某个值第一次出现的位置
public int indexOf(T t) {
Node node = first;
for (int index = 0; index < N; index++) {
node = node.next;
if (node.item.equals(t)) {
return index;
}
}
return -1;
}
//删除
public T remove(int i) {
//获取i位置的前一个结点
Node pre = first;
for (int index = 0; index < i - 1; index++) {
pre = pre.next;
}
//找到i位置的节点
Node currentNode = pre.next;
//获取i位置的下一个节点
Node nextNode = currentNode.next;
//让i位置的前一个节点的下一个结点变为i位置的下一个结点
pre.next = nextNode;
//让i位置的后一个节点的前一个结点变为i位置的上一个结点
nextNode.pre = pre;
//个数-1
N--;
return currentNode.item;
}
//获取首结点的值
public T getFirst() {
if (!isEmpty()) {
return first.next.item;
}
return null;
}
//获取尾节点的值
public T getLast() {
if (!isEmpty()) {
return last.item;
}
return null;
}
}
测试类
package cn.test.algorithm.test;
import cn.test.algorithm.datastruct.TwoWayLinkList;
public class TwoWayLinkListTest {
public static void main(String[] args) {
TwoWayLinkList<Integer> link = new TwoWayLinkList<>();
System.out.println("---------------------正常插入-------------------------");
link.insert(1);
link.insert(2);
link.insert(3);
link.insert(4);
System.out.println("首节点元素:"+link.getFirst());
System.out.println("尾节点元素:"+link.getLast());
System.out.println(link.toString());
for (Integer integer : link) {
System.out.println("遍历值:" + integer);
}
System.out.println("--------------------指定位置插入--------------------------");
link.insert(5, 1);
System.out.println("首节点元素:"+link.getFirst());
System.out.println("尾节点元素:"+link.getLast());
System.out.println(link.toString());
for (Integer integer : link) {
System.out.println("遍历值:" + integer);
}
System.out.println("---------------------获取操作-------------------------");
System.out.println("获取第三个位置元素:"+link.get(3));
System.out.println("获取值5的索引:"+link.indexOf(5));
System.out.println("-------------------删除第二个元素---------------------------");
//删除第二个位置的元素
link.remove(2);
System.out.println("首节点元素:"+link.getFirst());
System.out.println("尾节点元素:"+link.getLast());
System.out.println(link.toString());
for (Integer integer : link) {
System.out.println("遍历值:" + integer);
}
System.out.println("---------------------清空-------------------------");
//清空
link.clear();
System.out.println("首节点元素:"+link.getFirst());
System.out.println("尾节点元素:"+link.getLast());
System.out.println(link.toString());
for (Integer integer : link) {
System.out.println("遍历值:" + integer);
}
}
}
运行结果
---------------------正常插入-------------------------
首节点元素:1
尾节点元素:4
TwoWayLinkList{first=cn.test.algorithm.datastruct.TwoWayLinkList$Node@4554617c, last=cn.test.algorithm.datastruct.TwoWayLinkList$Node@74a14482, N=4}
遍历值:1
遍历值:2
遍历值:3
遍历值:4
--------------------指定位置插入--------------------------
首节点元素:5
尾节点元素:4
TwoWayLinkList{first=cn.test.algorithm.datastruct.TwoWayLinkList$Node@4554617c, last=cn.test.algorithm.datastruct.TwoWayLinkList$Node@74a14482, N=5}
遍历值:5
遍历值:1
遍历值:2
遍历值:3
遍历值:4
---------------------获取操作-------------------------
获取第三个位置元素:3
获取值5的索引:0
-------------------删除第二个元素---------------------------
首节点元素:5
尾节点元素:4
TwoWayLinkList{first=cn.test.algorithm.datastruct.TwoWayLinkList$Node@4554617c, last=cn.test.algorithm.datastruct.TwoWayLinkList$Node@74a14482, N=4}
遍历值:5
遍历值:2
遍历值:3
遍历值:4
---------------------清空-------------------------
首节点元素:null
尾节点元素:null
TwoWayLinkList{first=cn.test.algorithm.datastruct.TwoWayLinkList$Node@4554617c, last=null, N=0}
4.3.4、Java中LinkedList实现
java中LinkedList集合也是使用的双向链表实现,并提供了增删改查的方法,下面我们根据源码查看是否满足如下要求:
①底层是否使用了双向链表
//插入
public boolean add(E e) {
linkLast(e);
return true;
}
//进入linkLast方法,从这里可以看出确实使用了双向链表
void linkLast(E e) {
final Node<E> l = last;
final Node<E> newNode = new Node<>(l, e, null);
last = newNode;
if (l == null)
first = newNode;
else
l.next = newNode;
size++;
modCount++;
}
②结点类是否有三个域
private static class Node<E> {
E item;
Node<E> next;
Node<E> prev;
Node(Node<E> prev, E element, Node<E> next) {
this.item = element;
this.next = next;
this.prev = prev;
}
}
存在三个域,E表示元素,next下一个结点,prev:前一个节点
4.3.5、链表时间复杂度分析
这里主要还是分析几个方法:
- get(int i):获取元素值,每次查询都要从链表头开始进行查找,所以时间复杂度为O(n)
- insert(T t,int t):插入指定位置元素,这里也是需要通过链表开头进行查找,所以随着元素的增多,查找的元素也比较多,时间复杂度为O(n)
- remove(int i):每一次移除,需要先找到i元素的前一个元素,然后完成删除操作,随着元素N的增多,查找的元素越多,时间复杂度为O(n)
相比顺序表,链表插入和删除的时间复杂度虽然是一样的,但是任然有很大的有优势,因为链表的物理地址是不连续的,所以不需要预留指定的存储空间,不需要进行扩展,不需要进行元素交换。
相比顺序表,链表的查询效率性能会比较低,因此,我们的程序中查询操作较多,建议使用顺序表,增删操作比较多,建议使用链表。
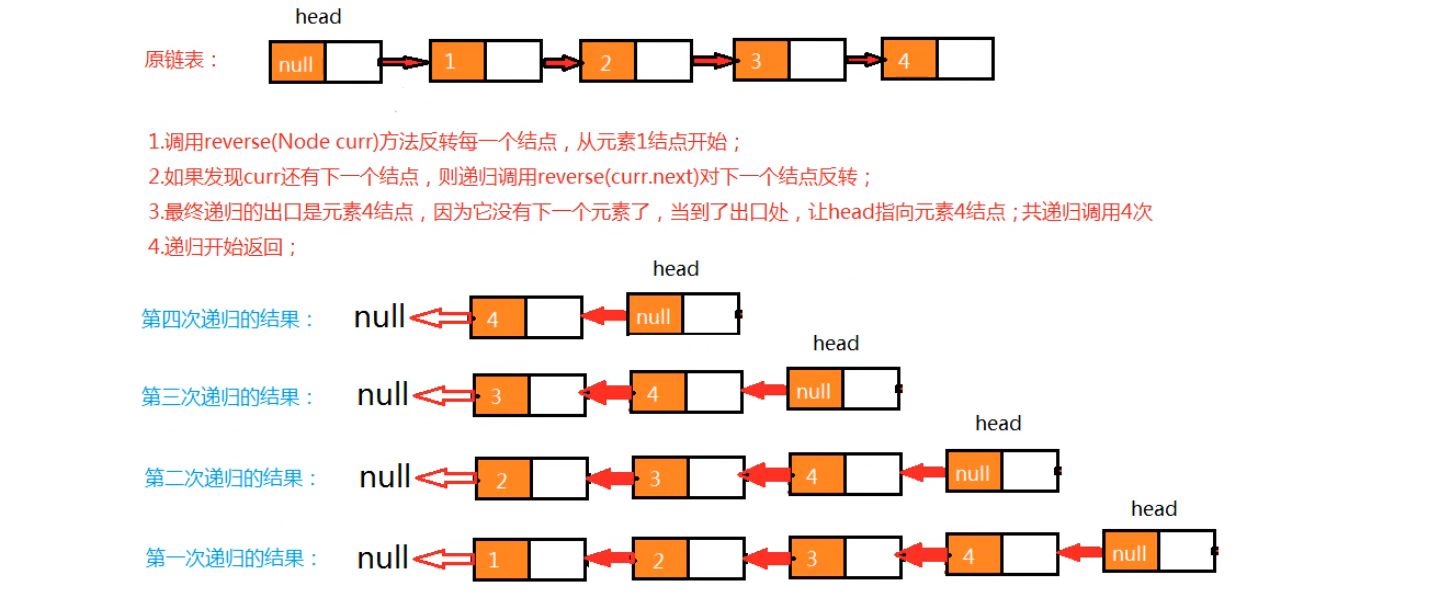
4.3.6、链表的反转
如何对链表进行反转,需求如下:
- 原链表:1->2->3->4
- 反转后:4->3->2->1
使用递归可以完成反转,递归反转其实就是从原链表的第一个存储数据的节点开始,一次递归调用反转的每一个节点,直到把最后一个结点反转完毕,整个链表就反转完毕。
API设计
- public void reverse():对整个链表反转
- public Node reverse(Node cur):反转链表中的某个结点curr,把反转后的curr结点返回。
实现类
//在LinkList类中添加如下两个方法
//反转整个链表啊
public void reverse() {
//判断当前链表是否为空
if (isEmpty()) {
return;
}
//不为空就进行结点反转调用
reverse(head.next);
}
//反转单个结点
public Node reverse(Node curr) {
//如果为空表示最后一个结点,需要首节点的next指向该结点
if (curr.next == null) {
head.next = curr;
return curr;
}
//递归反转当前结点的下一个结点,返回值就是链表反转后当前结点的上一个结点
Node pre = reverse(curr.next);
//将返回的节点的下一个结点编程当前结点
pre.next = curr;
//需要将curr的下一个结点变成null
curr.next = null;
return curr;
}
测试类
package cn.test.algorithm.test;
import cn.test.algorithm.datastruct.LinkList;
public class TestLinkList {
public static void main(String[] args) {
LinkList<Integer> link = new LinkList<>();
link.insert(1);
link.insert(2);
link.insert(3);
link.insert(4);
System.out.println(link.toString());
for (Integer integer : link) {
System.out.println("遍历值:" + integer);
}
System.out.println("---------------链表反转-----------------");
link.reverse();
System.out.println(link.toString());
for (Integer integer : link) {
System.out.println("遍历值:" + integer);
}
}
}
返回结果
LinkList{head=cn.test.algorithm.datastruct.LinkList$Node@4554617c, N=4}
遍历值:1
遍历值:2
遍历值:3
遍历值:4
---------------链表反转-----------------
LinkList{head=cn.test.algorithm.datastruct.LinkList$Node@4554617c, N=4}
遍历值:4
遍历值:3
遍历值:2
遍历值:1
4.3.7、快慢指针
快慢指针是定义两个指针,这两个指针移动的速度一快一慢,一次来制造出自己想要的差值,这个差值可以让我们找到链表上相应的节点。一般情况下快指针的移动步长是慢指针的两倍。
4.3.7.1、中间值问题
如下的测试类
package cn.test.algorithm.test;
public class SlowFastTest {
public static void main(String[] args) {
Node<String> node1 = new Node<>("node1", null);
Node<String> node2 = new Node<>("node2", null);
Node<String> node3 = new Node<>("node3", null);
Node<String> node4 = new Node<>("node4", null);
Node<String> node5 = new Node<>("node5", null);
Node<String> node6 = new Node<>("node6", null);
Node<String> node7 = new Node<>("node7", null);
node1.next = node2;
node2.next = node3;
node3.next = node4;
node4.next = node5;
node5.next = node6;
node6.next = node7;
//查找中间值
String mid = getMid(node1);
System.out.println("中间值为:" + mid);
}
//获取中间值
public static String getMid(Node<String> first) {
return null;
}
//结点类
private static class Node<T> {
T item;//结点
//下一个结点
Node next;
public Node(T item, Node next) {
this.item = item;
this.next = next;
}
}
}
需求:请完成测试类Test中的getMid方法,可以找出链表的中间元素值并返回。
利用快慢指针,我们把链表可以看成一个跑到,假设a的速度是b的两倍,那么当a跑完全程后,b刚好跑了一半,以此来达到目的。
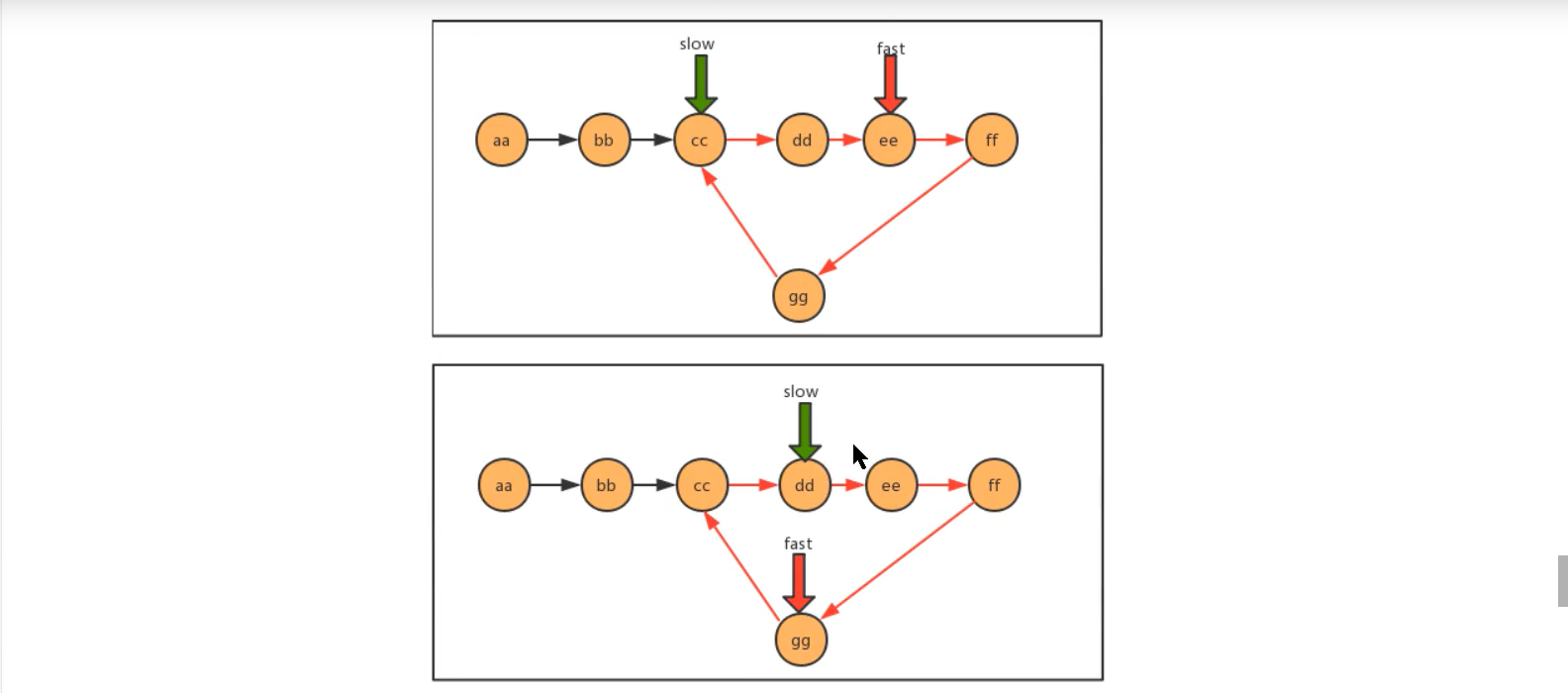
如下图,最开始,slow和fast指针都指向链表第一个结点,然后slow每次移动一个指针,fast每次移动两个指针。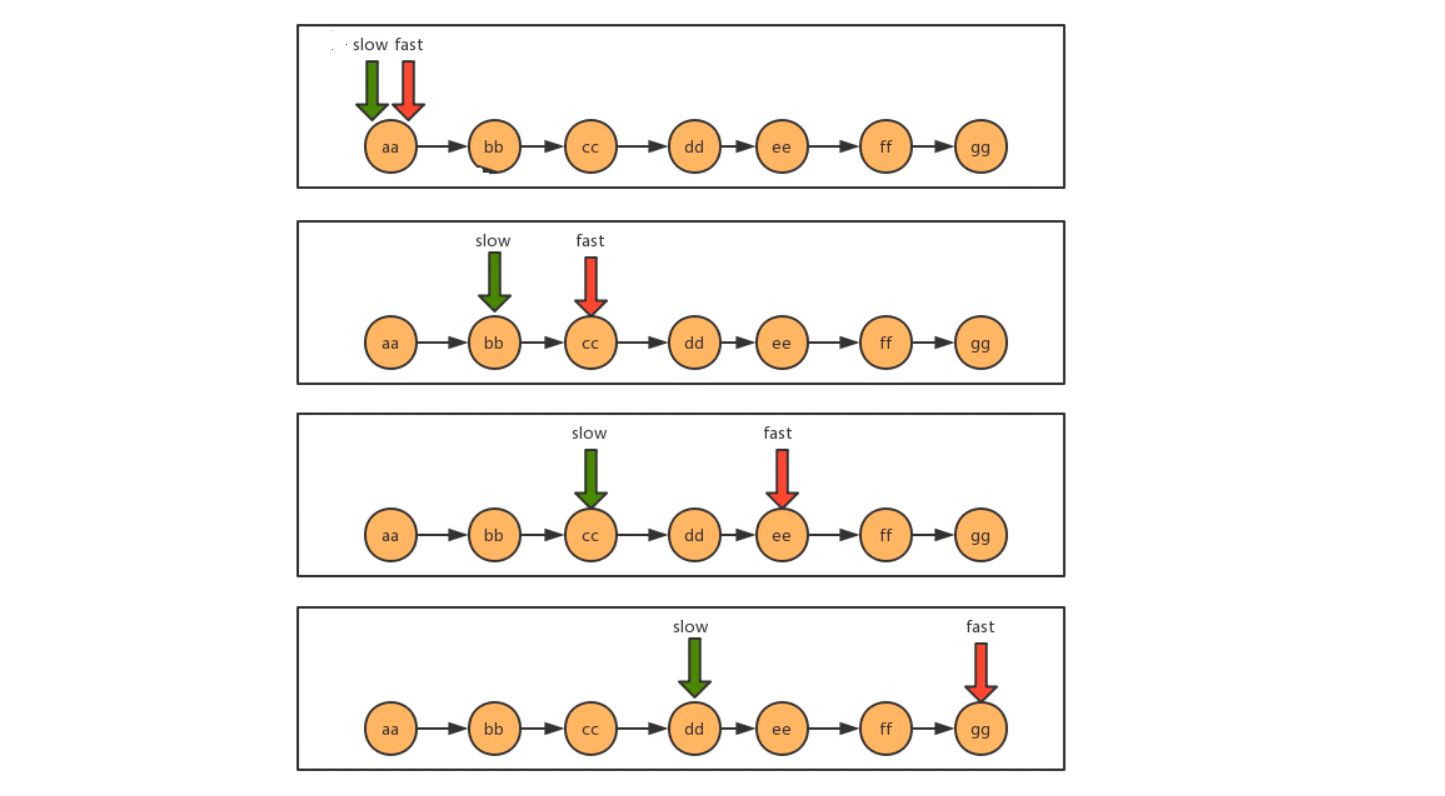
getMid的实现方式,如下:
public static String getMid(Node<String> first) {
//定义两个指针,都指向第一个结点
Node<String> fast = first;
Node<String> slow = first;
//需要遍历链表,当快指针指向的节点没有下一个结点就结束
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
}
//只需要返回慢指针的节点就是中间值
return slow.item;
}
运行结果:
中间值为:node4
4.3.7.2、单向链表是否有环问题
- 无环链表:快慢指针不会相遇
- 有环链表:快慢指针会相遇
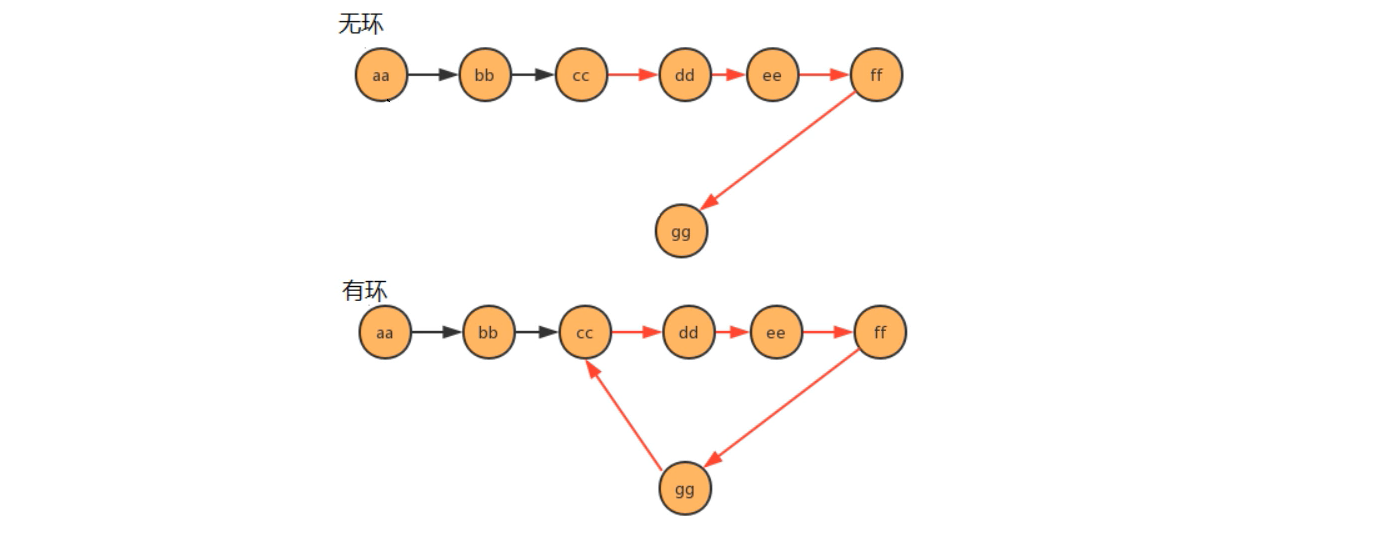
根据下面代码,完成需求:
package cn.test.algorithm.test;
public class CircleTest {
public static void main(String[] args) {
Node<String> node1 = new Node<>("node1", null);
Node<String> node2 = new Node<>("node2", null);
Node<String> node3 = new Node<>("node3", null);
Node<String> node4 = new Node<>("node4", null);
Node<String> node5 = new Node<>("node5", null);
Node<String> node6 = new Node<>("node6", null);
Node<String> node7 = new Node<>("node7", null);
node1.next = node2;
node2.next = node3;
node3.next = node4;
node4.next = node5;
node5.next = node6;
node6.next = node7;
//将node7结点指向node3
node7.next = node3;
//是否有环
Boolean isCircle = isCircle(node1);
System.out.println("链表是否有环:" + isCircle);
}
//判断链表是否有环
public static Boolean isCircle(Node<String> first) {
return false;
}
//结点类
private static class Node<T> {
T item;//结点
//下一个结点
Node next;
public Node(T item, Node next) {
this.item = item;
this.next = next;
}
}
}
需求:
请完善测试类CircleTest类中的isCircle方法,返回链表中是否有环。
使用快慢指针思想,还是把链表作为一个跑道,链表中又环,那么这条跑道就是一个圆环跑道,在一条圆环跑道中,两个人有速度差,那么迟早两人会相遇,相遇说明就是有环。
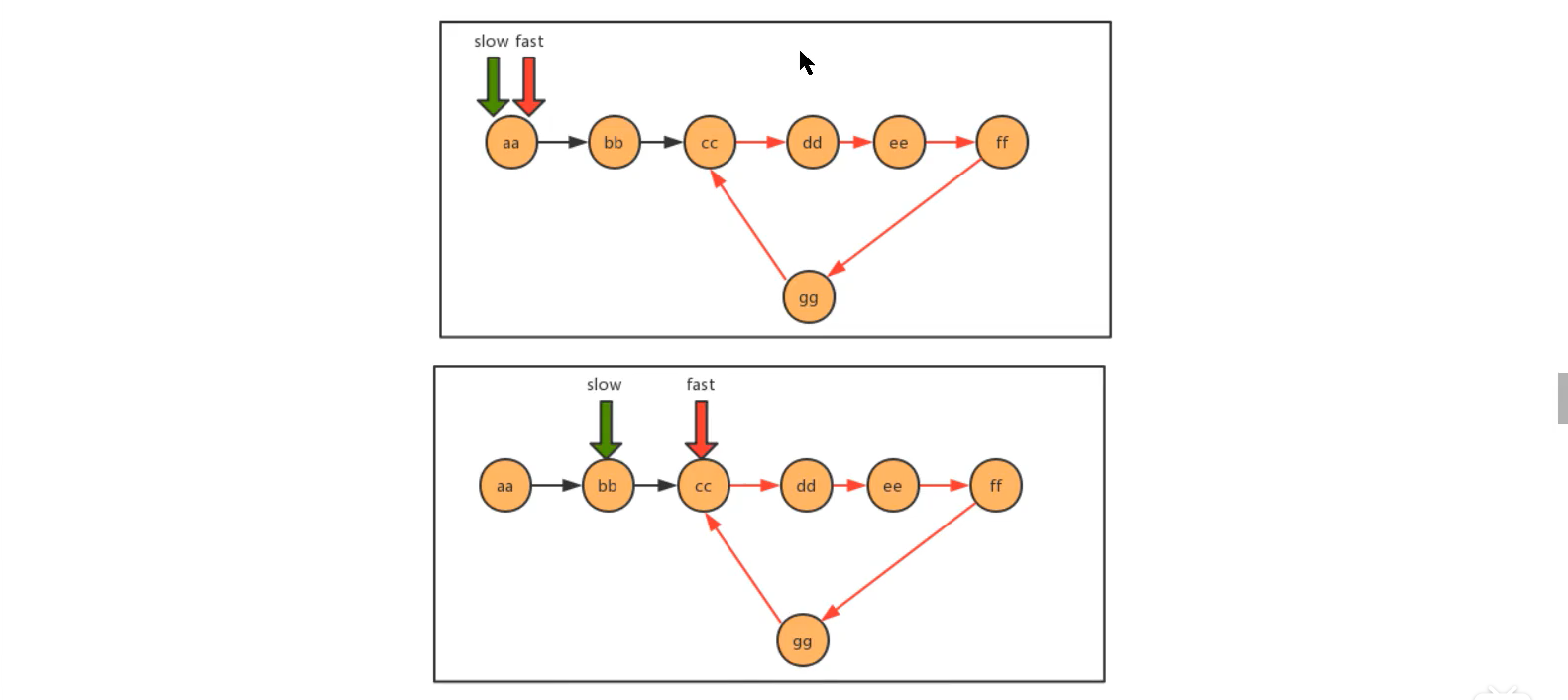
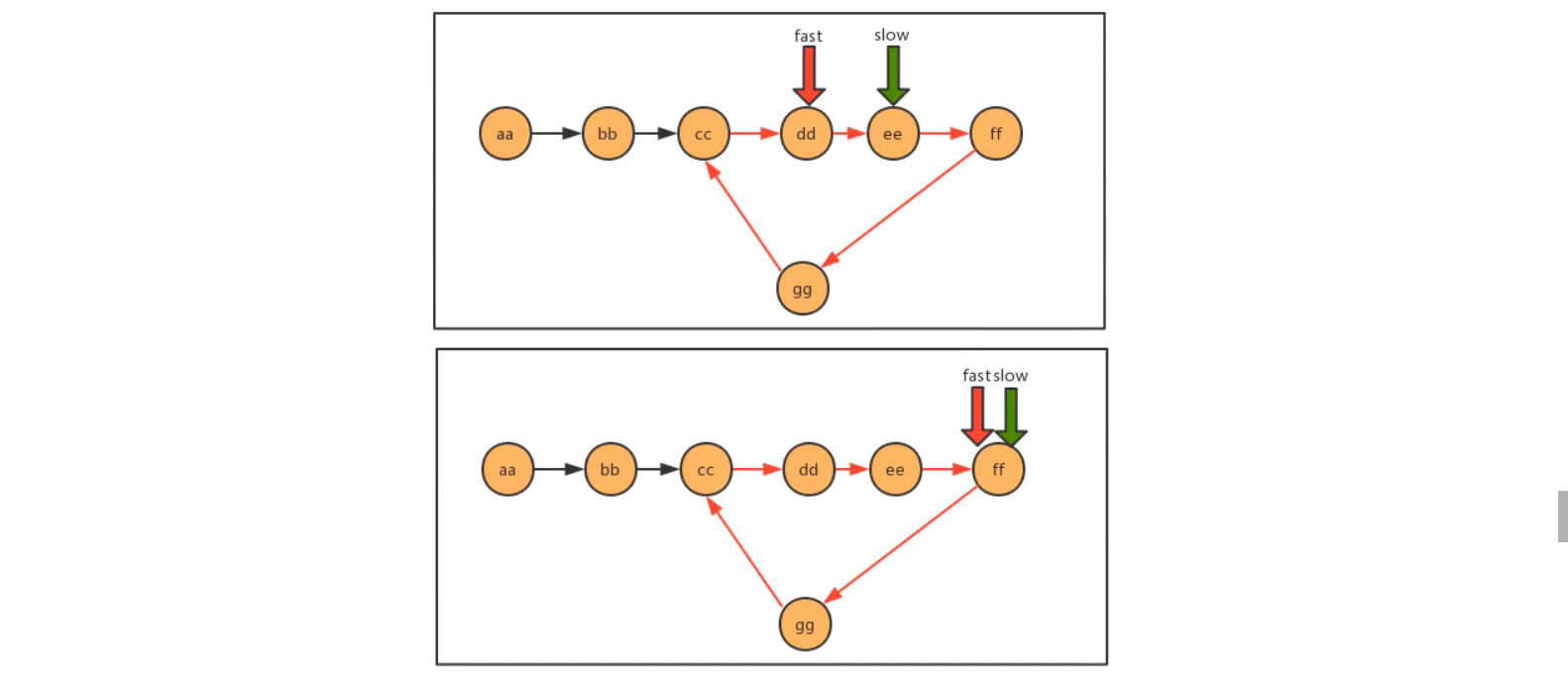
方法实现:
public static Boolean isCircle(Node<String> first) {
//定义快慢指针
Node<String> fast = first;
Node<String> slow = first;
//遍历链表,如果快慢指针指向了同一个结点,那么证明有环
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) {
return true;
}
}
return false;
}
运行结果:
链表是否有环:true
//屏蔽掉node7.next = node3;后运行
链表是否有环:false
4.3.7.3、有环链表入口问题
需求代码如下:
package cn.test.algorithm.test;
public class CircleEnterTest {
public static void main(String[] args) {
Node<String> node1 = new Node<>("node1", null);
Node<String> node2 = new Node<>("node2", null);
Node<String> node3 = new Node<>("node3", null);
Node<String> node4 = new Node<>("node4", null);
Node<String> node5 = new Node<>("node5", null);
Node<String> node6 = new Node<>("node6", null);
Node<String> node7 = new Node<>("node7", null);
node1.next = node2;
node2.next = node3;
node3.next = node4;
node4.next = node5;
node5.next = node6;
node6.next = node7;
//将node7结点指向node3
node7.next = node3;
//是否有环
Node<String> enter = circleEnter(node1);
if (enter != null) {
System.out.println("有环链表入口值:" + enter.item);
} else {
System.out.println("不是有环链表");
}
}
//有环链表入口结点
public static Node<String> circleEnter(Node<String> first) {
return null;
}
//结点类
private static class Node<T> {
T item;//结点
//下一个结点
Node next;
public Node(T item, Node next) {
this.item = item;
this.next = next;
}
}
}
当快慢指针相遇时,可以判断链表是否有环,这时候重新定义一个新的指针指向链表的起点,且步长跟慢指针一样为1,则慢指针与新指针相遇的地方就是环的入口,这个证明过程需要设计数论的知识,所以这里就不说明,只展示实现。
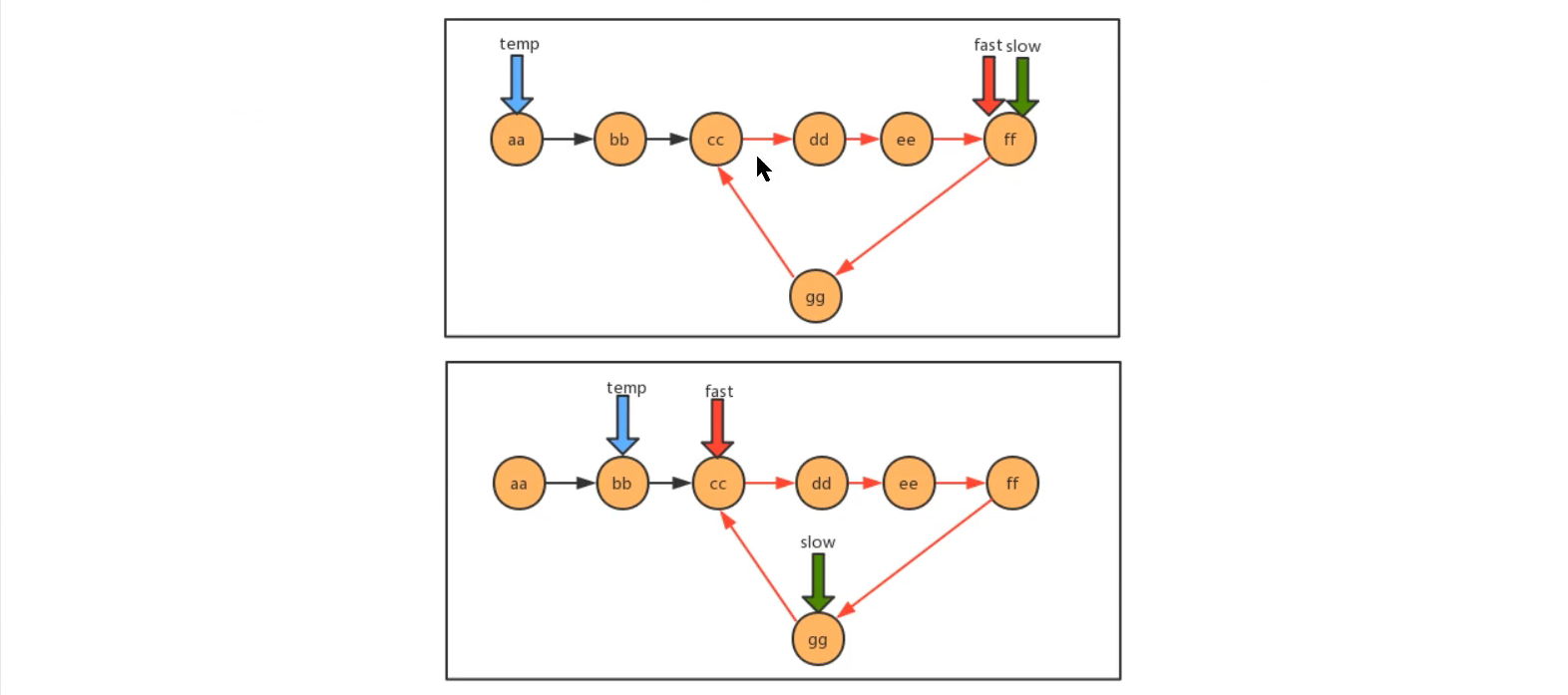
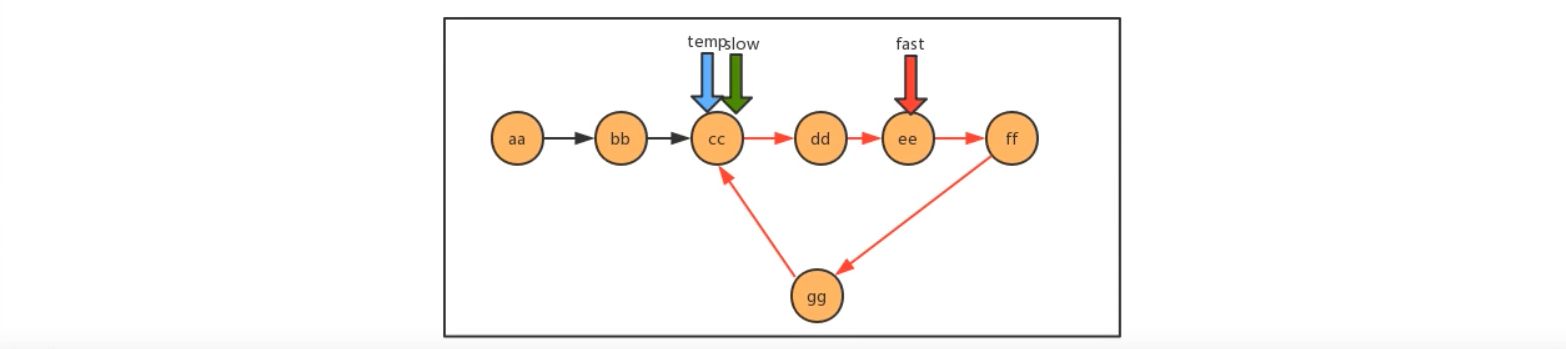
方法实现:
//有环链表入口结点
public static Node<String> circleEnter(Node<String> first) {
//定义快慢指针
Node<String> fast = first;
Node<String> slow = first;
Node<String> tmp = null;
//遍历找到是否是有环链表
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
//快慢指针相遇,临时指针指向首结点
if (fast == slow && tmp == null) {
tmp = first;
continue;
}
//临时指针变换
if (tmp != null) {
tmp = tmp.next;
//判断临时指针和慢指针相遇
if (tmp.equals(slow)) {
return tmp;
}
}
}
return null;
}
运行结果:
有环链表入口值:node3
4.3.8、循环链表
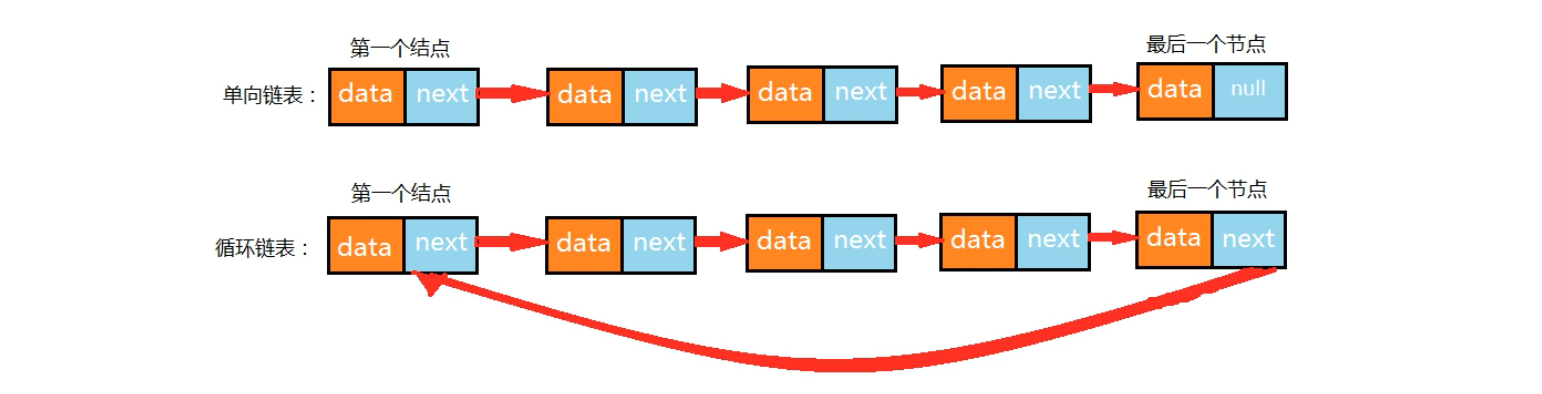
循环链表就是链表整体要形成一个圆环形,在单向链表中,我们最后一个结点指针是null,不指向任何结点,那么要实现循环链表,那么最后一个结点就要指向头结点。
循环链表实现:
package cn.test.algorithm.datastruct;
//循环链表
public class CircleLinkList {
public static void main(String[] args) {
Node<String> node1 = new Node<>("node1", null);
Node<String> node2 = new Node<>("node2", null);
Node<String> node3 = new Node<>("node3", null);
Node<String> node4 = new Node<>("node4", null);
Node<String> node5 = new Node<>("node5", null);
Node<String> node6 = new Node<>("node6", null);
Node<String> node7 = new Node<>("node7", null);
node1.next = node2;
node2.next = node3;
node3.next = node4;
node4.next = node5;
node5.next = node6;
node6.next = node7;
//将node7结点指向node3
node7.next = node3;
}
//结点类
private static class Node<T> {
T item;//结点
//下一个结点
Node next;
public Node(T item, Node next) {
this.item = item;
this.next = next;
}
}
}
4.3.9、约瑟夫问题
问题描述:在罗马人占领乔塔特后,39 个犹太人与Josephus及他的朋友躲到一个洞中,39个犹太人决定宁愿死也不要被敌人抓到,于是决定了一个自杀方式,41个人排成一个圆圈,由第1个人开始报数,每报数到第3人该人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从,Josephus要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,于是逃过了这场死亡游戏。
问题转换:
- 41个人坐一圈,第一个人编号为1,第二个人编号为2,第n个人编号为n;
- 编号为1的人开始从1报数,依次向后报数,报数为3的那个人退出;
- 自退出的那个人开始的下一个人开始从1开始报数,依次类推;
- 求出最后退出的那个人的编号;
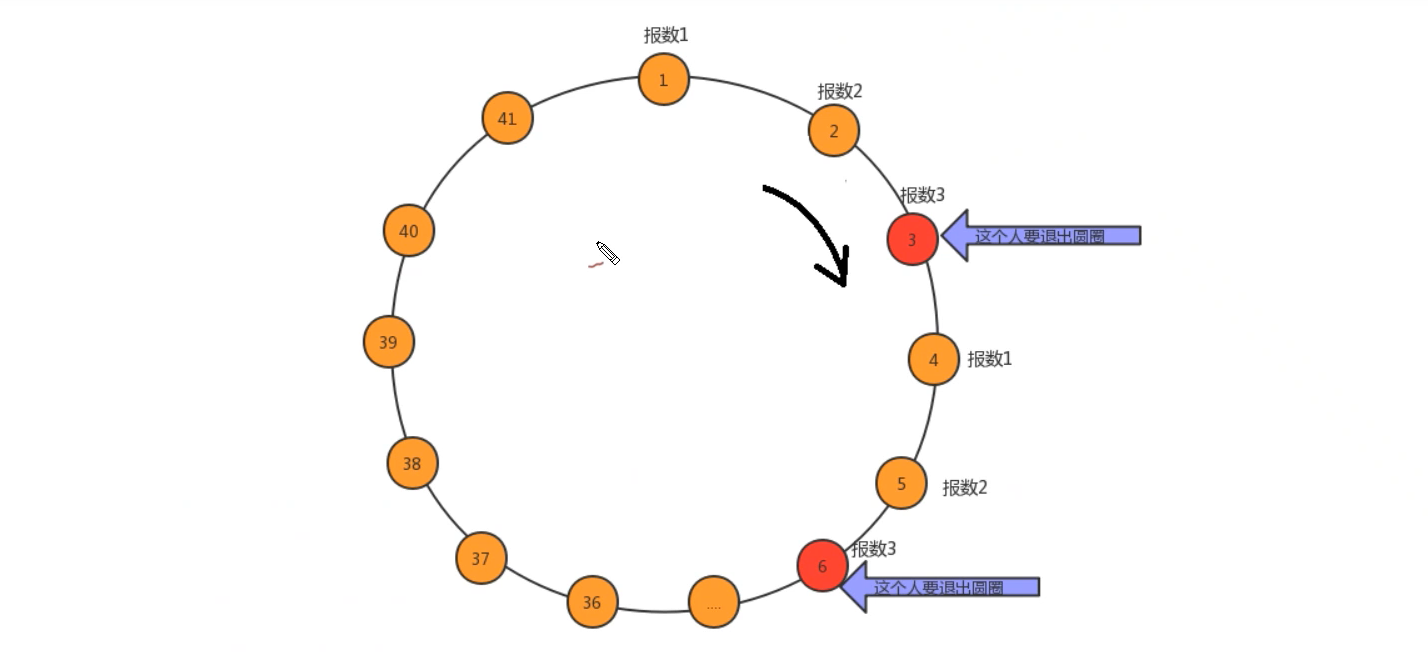
解题思路:
- 构件含有41个节点的单向循环链表,分别存储1-41的值,分别代表着41个人;
- 使用计数器count,记录当前报数的值
- 遍历链表,每循环一次,count++
- 判断count的值,如果是3,则从链表中删除这个节点并打印节点的值,把count的值重置为0
实现类:
package cn.test.algorithm.test;
public class JosephusTest {
public static void main(String[] args) {
//构件循环链表包含41个节点,分别存储1-41的值
//首结点
Node<Integer> first = null;
//记录前一个结点
Node<Integer> pre = null;
for (int i = 1; i <= 41; i++) {
Node<Integer> node = new Node<>(i, null);//初始化新结点
if (i == 1) {//第一个结点
first = node;
} else {
pre.next = node;
}
pre = node;
//如果是最后一个结点
if (i == 41) {
pre.next = first;
}
}
//打印
Node<Integer> node = first;
System.out.print("结点数据:【");
for (int i = 0; i < 41; i++) {
System.out.print(node.item + ",");
node = node.next;
}
System.out.println("】");
//计数器count,进行计数
int count = 0;
//遍历循环链表
Node<Integer> n = first;//记录每次遍历的结点,默认从首结点开始
Node<Integer> before = null;//记录当前结点的上一个结点
System.out.print("删除结点:【");
while (n != n.next) {
//模拟报数
count++;
//判断当前报数是不是3
if (count == 3) {
//如果是3,把当前结点删除,打印当前结点,重置count=0,当前结点下一一位
System.out.print(n.item + ",");
before.next = n.next;
count = 0;
} else {
//如果不是3,只需要让当前结点后移一位,当前结点的before变为当前结点
before = n;
}
n = n.next;
}
System.out.println(n.item + "】");
}
//结点类
private static class Node<T> {
T item;//结点
//下一个结点
Node next;
public Node(T item, Node next) {
this.item = item;
this.next = next;
}
}
}
运行结果:
结点数据:【1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,】
删除结点:【3,6,9,12,15,18,21,24,27,30,33,36,39,1,5,10,14,19,23,28,32,37,41,7,13,20,26,34,40,8,17,29,38,11,25,2,22,4,35,16,31】