归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用了分治思想的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列间有序。如果将两个有序表合并成一个有序表,称为二路归并。
3.5.1、需求
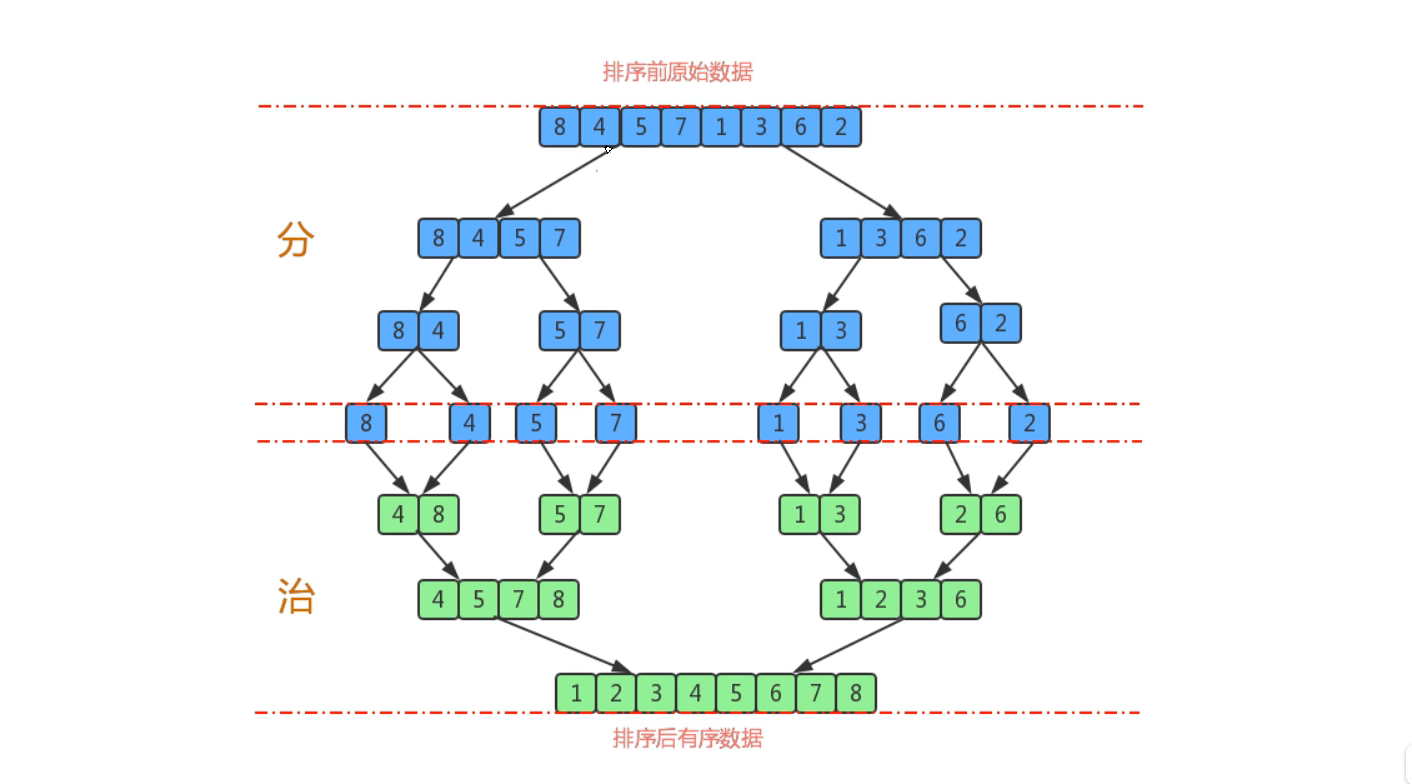
- 排序前:{8, 4, 5, 7, 1, 3, 6, 2}
- 排序后:{1, 2, 3, 4, 5, 6, 7, 8}
3.5.2、排序原理
- 尽可能的将一组数据拆分成两个元素相等的子组,并对每个子组继续进行拆分,知道拆分后的每个子组的元素个数是1为止
- 将相邻的两个子组进行合并成一个有序的大组
- 不断的重复步骤2,知道最终只有一个组为止
3.5.3、API设计
| 类名 | Merge |
|---|---|
| 构造方法 | Merge():创建Merge对象 |
| 成员方法 | public static void sort(Comparable[] a):对数组内的元素进行排序 private static void sort(Comparable[] a,int lo,int hi):对数组a中从索引lo到索引hi之间的元素进行排序 private static void merge(Compareble[] a,int lo,init mid,int hi):从索引lo到索引mid为一个子组,从索引mid+1到索引hi为另一个子组,把数组a的这个两个子组数据合成一个有序的大组(从索引lo到索引hi) private static boolean grater(Comparable v,Comparable w):判断v是否大于w private static void exch(Comparable[] a,int i,int j):交换a数组中,索引i和索引j处的值 |
| 成员变量 | private static Comparable[] assist:完成归并操作需要的辅助数组 |
3.5.4、代码实现
算法类:
package cn.test.algorithm.sort;
public class Merge {
private static Comparable[] assist;
/**
* 对数组元素进行排序
*
* @param a
*/
public static void sort(Comparable[] a) {
//初始化辅助数组
assist = new Comparable[a.length];
//定义一个lo变量,和hi变量,分别记录数组中最小的索引和最大的索引
int lo = 0;
int hi = a.length - 1;
//调用sort重载方法完成数组a中,从索引lo到索引hi的元素进行排序
sort(a, lo, hi);
}
//对lo到hi的元素进行排序
private static void sort(Comparable[] a, int lo, int hi) {
//安全性校验
if (hi <= lo) {
return;
}
//对lo到hi的数据进行分组
int mid = lo + (hi - lo) / 2;//mid作为中间值,分割数组
//分组后对每组数据进行排序
sort(a, lo, mid);
sort(a, mid + 1, hi);
//排序后对数据进行归并
merge(a, lo, mid, hi);
}
//合并数组并排序
private static void merge(Comparable[] a, int lo, int mid, int hi) {
//这里需要三个指针
int i = lo;//辅助数组的开始位置指针
int p1 = lo;//左边数组的开始位置指针
int p2 = mid + 1;//右边数组的开始位置指针
//对左右数组的数据进行比较,并插入到辅助数组中
while (p1 <= mid && p2 <= hi) {
if (greater(a[p1], a[p2])) {
assist[i++] = a[p2++];
} else {
assist[i++] = a[p1++];
}
}
//需要判断左边数组是否都移动完了
while (p1 <= mid) {
assist[i++] = a[p1++];
}
//需要判断右边数组是否都移动完了
if (p2 <= hi) {
assist[i++] = a[p2++];
}
//需要将辅助数组的数据复制到原数组中
for (int index = lo; index <= hi; index++) {
a[index] = assist[index];
}
}
/**
* 比较v元素是否大于w元素
*
* @return
*/
private static boolean greater(Comparable v, Comparable w) {
return v.compareTo(w) > 0;
}
/**
* 交换i和j处的元素值
*
* @param a
* @param i
* @param j
*/
private static void exch(Comparable[] a, int i, int j) {
Comparable temp;
temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
测试类:
package cn.test.algorithm.test;
import cn.test.algorithm.sort.Merge;
import java.util.Arrays;
public class MergeTest {
public static void main(String[] args) {
Integer[] arr = {8, 4, 5, 7, 1, 3, 6, 2};
Merge.sort(arr);
System.out.println(Arrays.toString(arr));
}
}
测试结果:
[1, 2, 3, 4, 5, 6, 7, 8]
3.5.5、时间复杂度分析
归并排序是分治思想的最典型的例子,上面的算法中,对a[lo….hi]进行排序,现将它分为a[lo…mid]和[mid+1…hi]两个部分,分别通过递归调用的方式对它们单独进行排序,最后将有序的子数组归并为最终的排序结果。该递归的出口在于如果一个数组不能再被分为两个子数组,那么就会执行merge进行归并,在归并的时候判断元素的大小进行排序。
如果一个数组有8个元素,那么它将每次除以2找到最小的子数组,共拆分log8,值为3,所以树共有三层,那么自顶向下第k层有2^k个子数组,每个数组的长度为2^(3-k),归并最多需要2^(3-k)次比较,因此每层需要比较次数为2^k*2^(3-k)=2^3,那么3层中共需要3*2^3;
假设元素的个数为n个,那么使用归并拆分次数为log(n),所以共log(n)层,那么使用log(n)替换上面的3*2^3这个层数,最终时间复杂度为:log(n)*2^(log(n))=log(n)*n,所以最终的复杂度为O(nlog(n));
归并排序的缺点:需要申请额外的空间,导致空间复杂度提升,最典型的就是以空间换时间操作。