4.9.1、堆的定义
堆(Heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵完全二叉树的数组对象。
堆的特性:
- 它是完全二叉树,除了树的最后一层结点不需要是满的,其他的每一层从左到右都是满的,如果最后一层结点不是满的,那么要求左满右不满
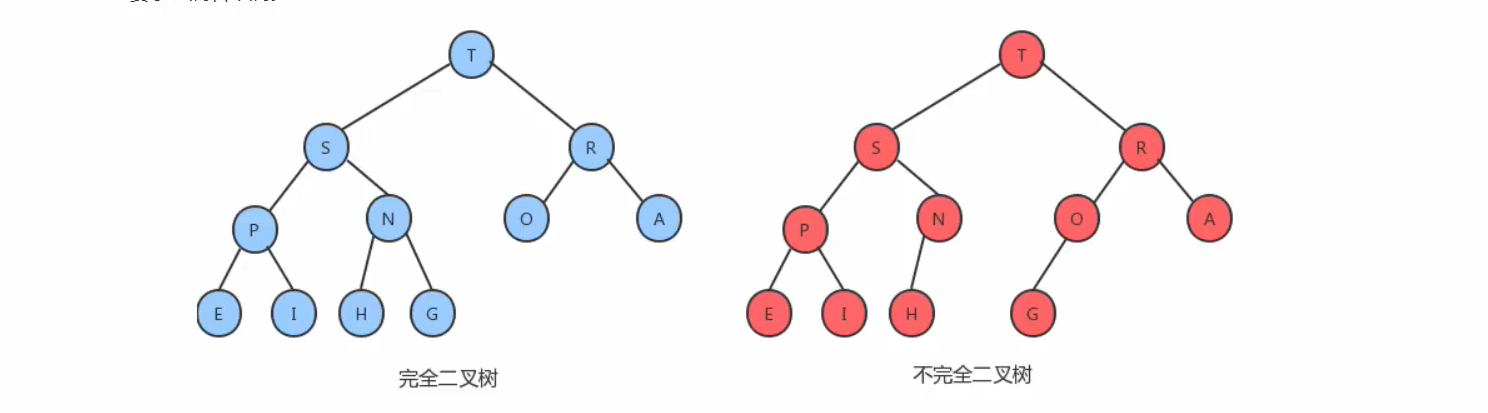
- 堆通常使用数组来实现
- 如果一个结点的位置为k,则它的父结点的位置为[k/2],而它的两个子结点的位置分别为2k和2k+1,在不使用指针的情况下,我们可以通过计算数组的索引在树中上下移动,从a[k]向上一层,就令k等于k/2下一层就令k等于2k或2k+1
- 每个结点都大于等于它的两个子节点,这里要注意堆中仅仅只规定每个结点大于等于它的两个子结点,但这两个子结点的顺序没有做规定,根学习的二叉查找树还是有区别的
4.9.2、堆的API设计
| 类名 | Heap |
|---|---|
| 构造方法 | Heap(int capacity):创建容量为capacity的堆对象 |
| 成员变量 | private T[] items:用来存储元素数组 private int N:记录堆中的元素个数 |
| 成员方法 | private boolean less(int i,int j):判断堆中索引i处的元素是否小于索引j处的元素 private void exch(int i,int j):交换索引i和索引j处的值 public T delMax():删除堆中最大的元素,并返回这个最大值 private void swim(int k):使用上浮算法,使索引k处的元素能在堆中处于一个正确的位置 private void sink(int k):使用下沉算法,使索引k处的元素能在堆中处于一个正确的位置 public void insert(T t):往堆中插入一个元素 |
4.9.3、堆的实现
实现类
package cn.test.algorithm.datastruct;
public class Heap<T extends Comparable<T>> {
//存放堆的元素
private T[] items;
//记录堆中元素个数
private int N;
public Heap(int capacity) {
this.items = (T[]) new Comparable[capacity + 1];
this.N = 0;
}
//比较索引i是否比索引j处值小
private boolean less(int i, int j) {
return items[i].compareTo(items[j]) < 0;
}
//交换索引i和j处的值
private void exch(int i, int j) {
T temp = items[i];
items[i] = items[j];
items[j] = temp;
}
//插入元素
public void insert(T t) {
items[++N] = t;//我们存值从1开始存,舍掉0处
swim(N);
}
//上浮算法
private void swim(int k) {
//通过循环不断比较当前结点的值与父结点的值,如果发现父结点的值小于当前结点就交换
while (k > 1) {
//比较当前结点和父结点
if (less(k / 2, k)) {
exch(k / 2, k);
}
k = k / 2;
}
}
//下沉算法
private void sink(int k) {
//通过循环不断对比当前k结点与左子结点2k和右子结点2k+1中的较大值比较,如果有就交换
while (2 * k < N) {
//当前结点的子结点的较大结点
int max;//记录较大结点所在的索引
if (2 * k + 1 <= N) {
if (less(2 * k, 2 * k + 1)) {
max = 2 * k + 1;
} else {
max = 2 * k;
}
} else {
max = 2 * k;
}
if (!less(k, max)) {
break;
}
exch(k, max);
//变换k的值为最大索引处的值
k = max;
}
}
//删除堆中最大的元素
public T delMax() {
T max = items[1];//第一个元素是最大值
//交换索引i和最大索引处的值
exch(1, N);
//最大索引处元素删掉
items[N] = null;
//元素个数-1
N--;
//通过下沉让堆重写有序
sink(1);
return max;
}
}
测试类
package cn.test.algorithm.test;
import cn.test.algorithm.datastruct.Heap;
public class HeapTest {
public static void main(String[] args) {
Heap<Integer> heap = new Heap<>(100);
heap.insert(1);
heap.insert(2);
heap.insert(3);
heap.insert(4);
heap.insert(5);
heap.insert(6);
heap.insert(7);
Integer result = null;
while (true) {
result = heap.delMax();
if (result == null) {
break;
}
System.out.println("删除最大值为:" + result);
}
}
}
测试结果
删除最大值为:7
删除最大值为:6
删除最大值为:5
删除最大值为:4
删除最大值为:3
删除最大值为:2
删除最大值为:1
4.9.4、堆排序
给定一个数组:
String[] arr = {"S","O","R","T","E","X","A","M","P","L","E"};
请对数组中的字符从小到大排序
4.9.4.1、堆排序API设计
| 类名 | HeapSort |
|---|---|
| 成员方法 | public static void sort(Comparable[] source):对source数组中的数据从小到大排序 private static void createHeap(Comparable[] source,Comparable[] heap):根据原数组source,构造出堆head private static boolean less(Comparable[] head,int i,int j):判断堆heap中索引i处的元素是否比索引j处的元素小 private static void exch(Comparable[] heap,int i,int j):交换堆head的i和j处的元素 private static void sink(Comparable[] heap,int target,int range):在heap堆中,对target处的元素做下沉,范围是0-range |
4.9.4.2、实现步骤
- 1、构造堆
- 2、获取堆顶元素,这个值就是最大值
- 3、交换堆顶元素和数组中的最后一个元素,此时所有元素中的最大元素已经放到了合适的位置
- 4、对堆进行调整,重写让除了最后一个元素的剩余元素中的最大值放到堆顶
- 5、重复上面2~4步骤,直到堆中剩下一个元素为止
4.9.4.3、实现过程
实现类
package cn.test.algorithm.datastruct;
public class HeapSort<T extends Comparable<T>> {
//比较堆i是否比j处的值小
private static boolean less(Comparable[] heap, int i, int j) {
return heap[i].compareTo(heap[j]) < 0;
}
//交换堆中i和j处的值
private static void exch(Comparable[] heap, int i, int j) {
Comparable tmp = heap[i];
heap[i] = heap[j];
heap[j] = tmp;
}
//根据数组创建对
private static void createHeap(Comparable[] source, Comparable[] heap) {
//把source的元素拷贝的heap中,这个是一个无序堆
System.arraycopy(source, 0, heap, 1, source.length);
//对堆的元素做下沉操作(从长度1的一半处开始,往索引1开始扫描,根据堆的特性来处理的)
for (int i = heap.length / 2; i >= 1; i--) {
sink(heap, i, heap.length - 1);
}
}
//从小到大排序
public static void sort(Comparable[] source) {
Comparable[] heap = new Comparable[source.length + 1];
createHeap(source, heap);
int N = heap.length - 1;
while (N != 1) {
//交换1和N处的元素
exch(heap, 1, N);
//个数减1
N--;
//下沉堆
sink(heap, 1, N);
}
//堆数组的元素拷贝到原数组
System.arraycopy(heap, 1, source, 0, source.length);
}
//下沉算法
private static void sink(Comparable[] heap, int target, int range) {
while (2 * target <= range) {
int max = 2 * target;
if (2 * target + 1 <= range) {
if (less(heap, 2 * target, 2 * target + 1)) {
max = 2 * target + 1;
}
}
if (!less(heap, target, max)) {
break;
}
exch(heap, target, max);
target = max;
}
}
}
测试类
package cn.test.algorithm.test;
import cn.test.algorithm.datastruct.HeapSort;
import java.util.Arrays;
public class HeapSortTest {
public static void main(String[] args) {
String[] arr = {"S", "O", "R", "T", "E", "X", "A", "M", "P", "L", "E"};
HeapSort.sort(arr);
System.out.println(Arrays.toString(arr));
}
}
测试结果
[A, E, E, L, M, O, P, R, S, T, X]