四点共圆模型
四点共圆:若在同一个平面内,有四个点在同一个圆上,则称这四个点共圆,一般简称“四点共圆”.
一、模型1:定点定长共圆模型(圆的定义)
若四个点到一个定点的距离相等,则这四个点共圆.如图,若OA=OB=OC=OD,则A,B,C,D四点在以点O为圆心、OA为半径的圆上.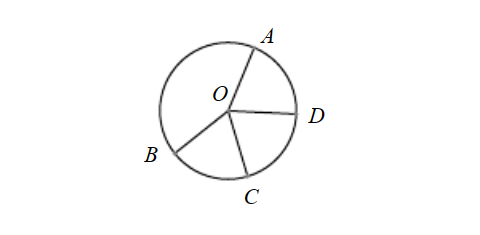
例1、如图,点O为线段BC的中点,点A、C、D到点O的距离相等,若∠ABC=40°,求∠ADC的度数.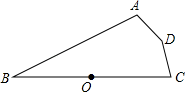
解:由题意得到OA=OB=OC=OD,作出圆O,如图所示,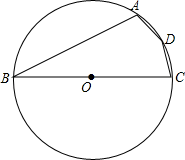
∴四边形ABCD为圆O的内接四边形,
∴∠ABC+∠ADC=180°,
∵∠ABC=40°,
∴∠ADC=140°。
例2、如图,四边形ABCD中,DA=DB=DC,∠BDC=72°,求∠BAC的度数.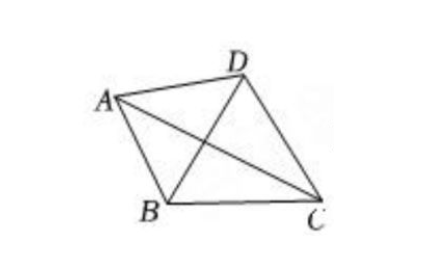
解:如图,∵DA=DB=DC,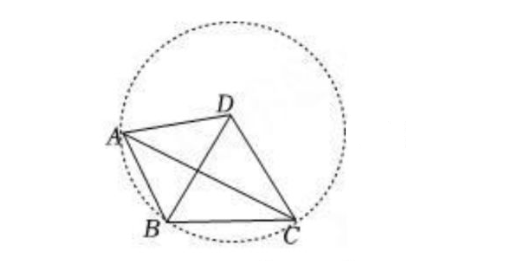
∴ A、B、C在以点D为圆心的圆上
∴ ∠BAC=\frac{1}{2}∠BDC=36°.
二、模型2:对角互补共圆模型
若一个四边形的一组对角互补,则这个四边形的四个顶点共圆.
如图,在四边形ABCD中, 若∠A+∠C=180°(或∠B+∠D=180°)则A,B,C,D四点在同一个圆上.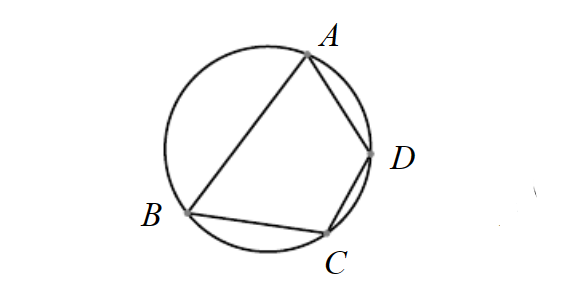
拓展:若一个四边形的外角等于它的内对角,则这个四边形的四个顶点共圆.
如图,在四边形ABCD中,∠CDE为外角,若∠B=∠CDE,则A,B,C,D四点在同一个圆上.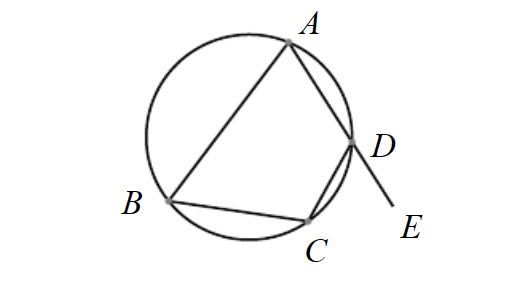
例1、已知:如图,四边形ABCD中,AC平分∠BAD,∠B+∠D=180°.求证:BC=CD.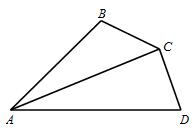
解:∵ ∠B+∠D=180°
∴ A、B、C、D四点共圆。
∵ AC平分∠BAD
∴ ∠DAC=∠CAB
∴ BC=CD
三、定边对双直角共圆模型
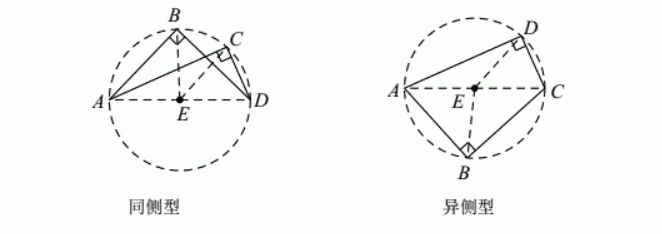
1、定边对双直角模型(同侧型)
若平面上A、B、C、D四点满足∠ABC=∠ACD=90°,则:A、B、C、D四点共圆,其中AD是直径.
2、定边对双直角模型(同侧型)
若平面上A、B、C、D四点满足∠ABC=∠ADC=90°,则:A、B、C、D四点共圆,其中AD是直径.
例1、如图,四边形ABCD中,AC=BC,∠ACB=90°,AD⊥BD于点D,若BD=2,CD=4\sqrt{2},求线段AB的长.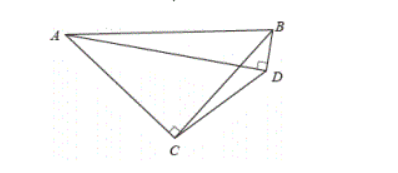
解:∵ ∠ACB=90°,AD⊥BD
∴ A、B、D、C四点共圆,且AB为直径
作CF⊥CD,交AD于点F,AD与CB交于点E,如图所示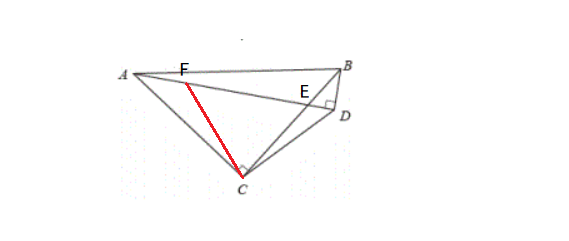
∵ ∠ABC=45°
∴ ∠ADC=45°,△CFD是等腰直角三角形
∴ FD=\sqrt{2}CD=8
∵ CD⊥CF
∴ CF=CD
∵ ∠CAF=∠CBD,AC=BC
∴ △AFC≌△CBD
∴ AF=BD=2
∴ AD=AF+FD=2+8=10
∴ AB=\sqrt{AD^2+BD^2}=\sqrt{10^2+2^2}=2\sqrt{26}
例2、如图,等腰Rt△ABC中,∠ACB=90°,D为BC上一点,连接AD。作BE⊥AD延长线与点E,连接CE,求证:∠AEC=45°.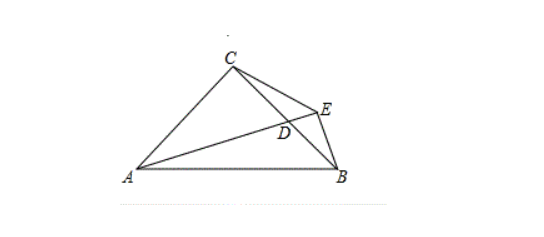
证明:∵ 等腰Rt△ABC中,∠ACB=90°
∴ AC=BC,∠ABC=∠CAB=45°
∵ BE⊥AD,∴ ∠AEB=90°
∵ ∠AEB=∠ACB
∴ A、B、E、C四点共圆
∴ ∠AEC=∠ABC=45°.
四、模型4:定弦定角共圆模型
若两个点在一条线段的同旁,并且和这条线段的两端连线所夹的角相等,那么这两个点和这条线段的两个端点共圆。
如图,点A,D在线段BC的同侧,若∠A=∠D,则A,B,C,D四点在同一个圆上.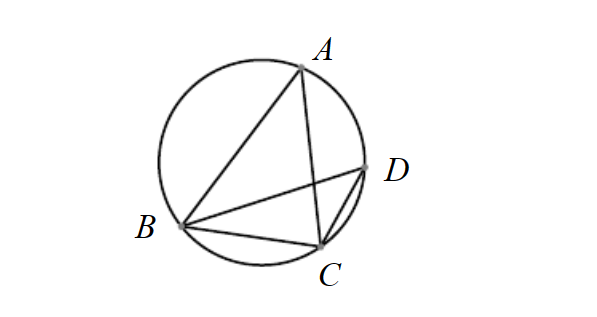
例1、如图,已知△ABC是等腰直角三角形,点D在线段BC上,四边形ADEF是正方形,连接FC,求证:FC⊥BC.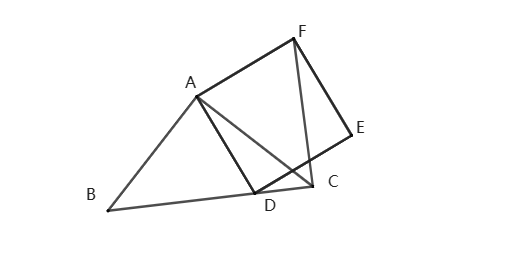
证明:如图,连接DF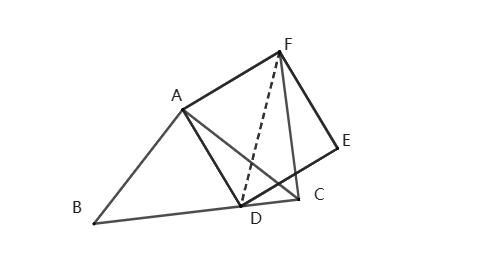
∵ 四边形ADEF是正方形
∴ ∠AFD=45°
∵ △ABC是等腰直角三角形
∴ ∠ACB=45°
∴ ∠AFD=∠ACB
∴ A、D、C、F四点共圆
∵ ∠FAD=90°,∠FAD+∠DCF=180°
∴ ∠FCD=90
∴ FC⊥BC.
例2、如图,在Rt△ABC中,∠BAD=90°,∠ABC=40°,将△ABC绕A点顺时针旋转得到△ADE,使D点落在BC边上.
(1)求∠BAD的度数;
(2)求证:A、D、B、E四点共圆.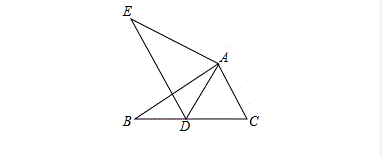
解:(1)∵ Rt△ABC中,∠BAD=90°,∠ABC=40°
∴ ∠C=50°
∵ 将△ABC绕A点顺时针旋转得到△ADE,使D点落在BC边上
∴ AD=AC
∴ ∠ADC=∠C=50°
∴ ∠ADC=∠ABC+∠BAD=50°
∴ ∠BAD=50°-40°=10°.
证明:(2)∵ 将△ABC绕A点顺时针旋转得到△ADE
∴ ∠AED=∠ABC
∴ A、D、B、E四点共圆.
 报错Electron failed to install correctly, please delete node_modules/electron and try installing again处理
报错Electron failed to install correctly, please delete node_modules/electron and try installing again处理 Towxml 是一个让小程序(微信/QQ)可以解析Markdown、HTML的解析库。能够使小程序完美解析Markdown内容。
Towxml 是一个让小程序(微信/QQ)可以解析Markdown、HTML的解析库。能够使小程序完美解析Markdown内容。 初中数学:平面直角坐标系中四边形面积求法
初中数学:平面直角坐标系中四边形面积求法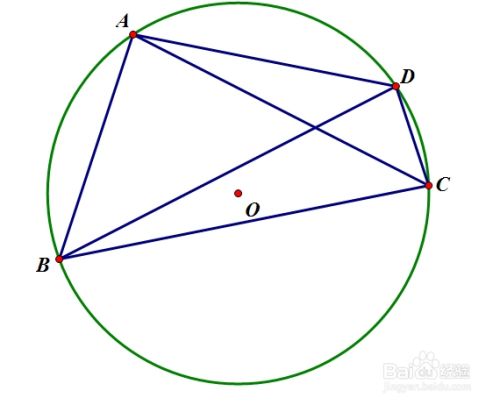 四点共圆:若在同一个平面内,有四个点在同一个圆上,则称这四个点共圆,一般简称“四点共圆”.
四点共圆:若在同一个平面内,有四个点在同一个圆上,则称这四个点共圆,一般简称“四点共圆”. 默认情况下 pip 使用的是国外的镜像,在下载的时候速度非常慢,本文我们介绍使用国内源对pip进行加速。
默认情况下 pip 使用的是国外的镜像,在下载的时候速度非常慢,本文我们介绍使用国内源对pip进行加速。 快速生成表格
快速生成表格 Docker编译镜像出现:fetch http://dl-cdn.alpinelinux.org/alpine/v3.12/main/x86_64/APKINDEX.tar.gz
ERROR: http://dl-cdn.alpinelinux.org/alpine/v3.12/main: temporary error (try again later)
WARNING: Ignoring APKINDEX.2c4ac24e.tar.gz: No such file or directory问题
Docker编译镜像出现:fetch http://dl-cdn.alpinelinux.org/alpine/v3.12/main/x86_64/APKINDEX.tar.gz
ERROR: http://dl-cdn.alpinelinux.org/alpine/v3.12/main: temporary error (try again later)
WARNING: Ignoring APKINDEX.2c4ac24e.tar.gz: No such file or directory问题 在Mac电脑中,如何对Git的用户名和密码进行修改呢?起初不懂Mac,所以整了很久,本文将记录如何对这个进行操作,以便后期使用。
在Mac电脑中,如何对Git的用户名和密码进行修改呢?起初不懂Mac,所以整了很久,本文将记录如何对这个进行操作,以便后期使用。 在使用Git的过程中,不想每次都输入用户名和密码去拉取代码,所以就需要保存这些信息,那么既然有保存了,就必须有清除功能。
在使用Git的过程中,不想每次都输入用户名和密码去拉取代码,所以就需要保存这些信息,那么既然有保存了,就必须有清除功能。