相似三角形模型——A字型和8字型模型
相似三角形是初中几何中非常重要的知识点,是中考中的常考题型,相似三角形是全等三角形的推广,全等可以理解是相似比为1的相似三角形。在相似三角形中也有一些固定的几何模型,这里我们主要讲述下相似三角形中的“A字型”和“8字型”模型。
这里先回顾下三角形相似的判定:
1、两角对应相等两个三角形相似。
2、两边成比例且夹角相等两个三角形相似。
3、三边成比例的两个三角形相似。
4、一条直角边与斜边成比例的两个直角三角形相似。
5、一个三角形两边去比另一个三角形与之相对应的两边,分别对应成比例,如果三组对应边相比都相同,则三角形相似。
模型一、A字型相似
1、平行A字型
模型:在△ABC中,DE//BC,则△ADE∽△ABC.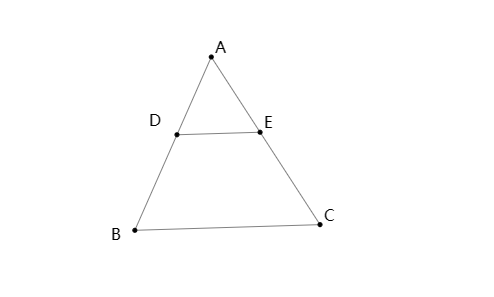
证明:∵ DE//BC
∴ ∠ADE=∠B,∠AED=∠C
∵ ∠A=∠A
∴ △ADE∽△ABC.
既然两个三角形相似,那么就有对应边成比例,则:
\frac{AD}{AB}=\frac{AE}{AC}=\frac{DE}{BC}.
(1)双A字或多A字模型
如图,在△ABC中,DE//BC.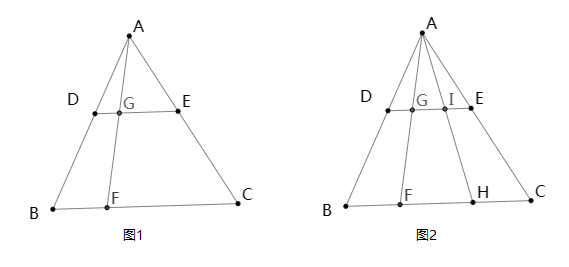
图1中,相似三角形有:
△ADE∽△ABC,△ADG∽△ABF,△AGE∽△AFC
∴ DG:GE=BF:FC
图2中,相似三角形就有很多了,则有:
∴ DG:BF=GI:FH=IE:HC
当然上面的模型可以继续推广下去,同样有相应的比例关系。
(2)三角形内接矩形模型
如图,在△ABC中,四边形DEGF是内接矩形,AH⊥BC.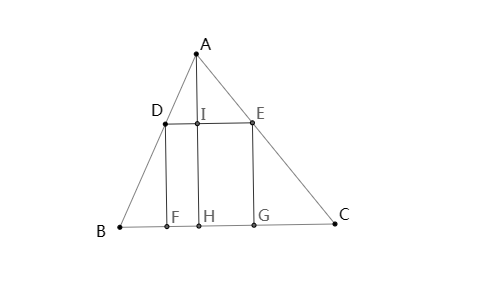
∵ 四边形DEGH为△ABC的内接矩形
∴ DE//BC,DF//AH//EG
∵ DE//BC
∴ △ADE∽△ABC,△ADI∽△ABH,△AIE∽△AHC
∵ DF//HI,DF⊥BC,AH⊥BC,AH⊥DE
∴ △BDF∽△DIA∽△BAH
∵ EG//AH,EG⊥BC,AH⊥BC,AH⊥DE
∴ △CEG∽△EAI∽△CAH
通过相似,找相似比,也就很容易了。
2、斜(反)A字型
如图,在△ABC中,∠B=∠AED,则△ADE∽△ABC.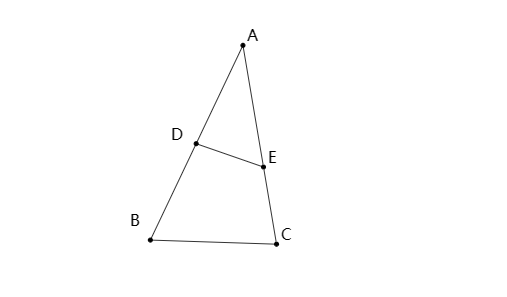
3、子母型(共边共角型)
如图,,在△ABC中,∠B=∠AED,则△ADE∽△ABC.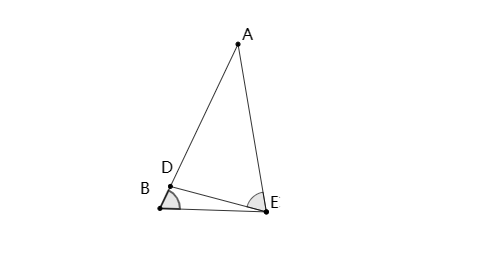
4、共角相似
如图,已知∠B=∠D,则:△ABC∽△ADE.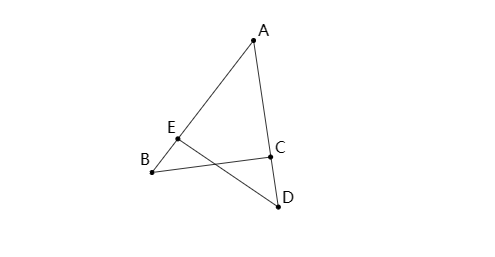
模型二、8字型(X字模型)
1、平行8字型
如图,AD//BC,则△ADE∽△BCD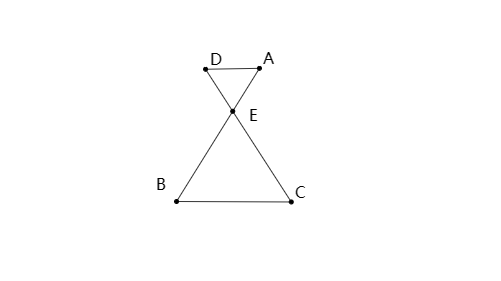
证明省略。该模型还可以继续推广到如下: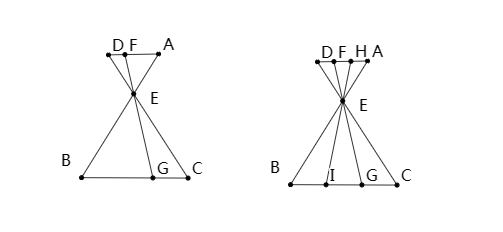
2、斜8字型(蝴蝶型)
如图,已知∠B=∠D,则△ABE∽△CDE.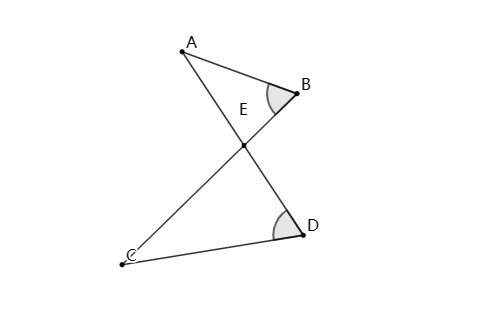
三、例题
例1、如图,已知DE//BC,CD和BE相交于点O,S_{△DOE}:S_{△COB}=4:9,求AE:EC的值.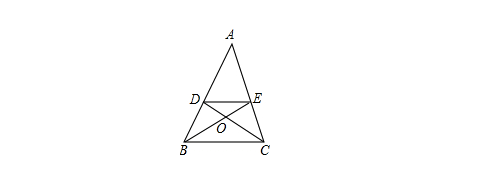
解:∵ DE//BC
∴ △ADE∽△ABC,△DOE∽△COB.
∵ S_{△DOE}:S_{△COB}=4:9
∴ △DOE和△COB的相似比为2:3,则:DE:BC=2:3.
∴ △ADE和△ABC的相似比也为2:3,
∴ AE:AC=2:3
∴ AE:EC=2:1
例2、如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,连接DE,EF,已知四边形BFED为平行四边形,DE:BC=1:4.若AB=8,求线段AD的长.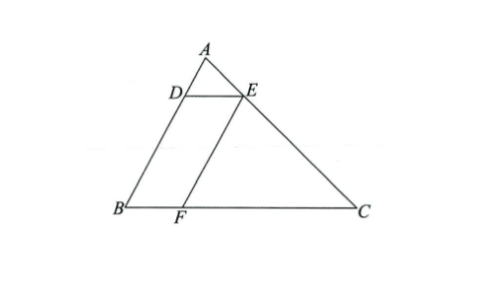
解:∵ 四边形BFED为平行四边形
∴ DE//BF
∴ DE//BC
∴ △ADE∽△ABC
∵ DE:BC=1:4
∴ AD:AB=1:4
∵ AB=8
∴ AD=2.
例3、如图,在△ABC中,点F、G在BC上,点E、H分别在AB、AC上,四边形EFGH是矩形,EH=2EF,AD是△ABC的高.BC=8,AD=6,求EH的长.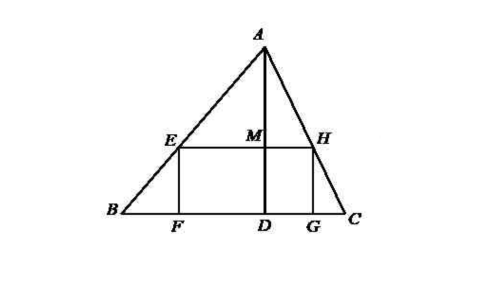
解:∵ 四边形EFGH是矩形
∴ DH//BC
∴ △AEH∽△ABC
∵ AM,AD分别为△AEH和△ABC的高
∴ \frac{AM}{AD}=\frac{EH}{BC}
∵ DM=EF
∴ AM=AD-DM=AD-EF=6-EF
∵ EF=2EF
∴ \frac{6-EF}{6}=\frac{2EF}{8}
解得:EF=\frac{12}{5}
∴ EH=2×\frac{12}{5}=\frac{24}{5}
例4、如图,已知在△ABC中,BE平分∠ABC交AC于点E,点D在BE的延长线上,且BA·BC=BD·BE.
(1)求证:△ABD∽△EBC;
(2)求证:AD^2=BD·DE.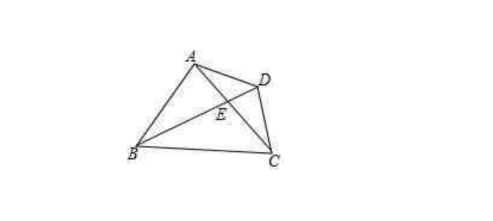
证明:(1)∵ BA·BC=BD·BE
∴ \frac{BA}{BD}=\frac{BE}{BC}
∵ BE平分∠ABC
∴ ∠ABD=∠EBC
∴ △ABD∽△EBC.
(2)∵ △ABD∽△EBC
∴ ∠BAD=∠BEC,∠ADB=∠BCE,
∵ ∠AED=∠BEC
∴ ∠EBC=∠DAD
∴ △ADE∽△BEC
∴ △AED∽△ABD
∴ \frac{AD}{BD}=\frac{DE}{AD}
即:AD^2=BD·DE.
例5、如图,AD于BC交于点O,EF过点O,交AB于点E,交CD于点F,BO=1,CO=3,AO=\frac{3}{2},DO=\frac{9}{2}.
(1)求证:∠A=∠D.
(2)若AE=BE,求证:CF=DF。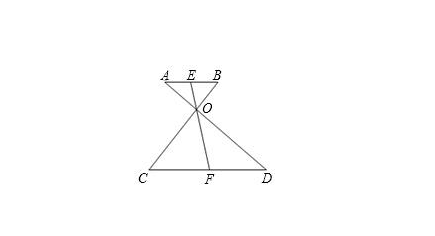
证明:(1)∵BO=1,CO=3,AO=\frac{3}{2},DO=\frac{9}{2}
∴ \frac{BO}{CO}=\frac{1}{3},
\frac{AO}{DO}=\frac{1}{3}
∴ \frac{BO}{CO}=\frac{AO}{DO}
∵ ∠AOB=∠DOC
∴ △OAB∽△OCD
∴ ∠A=∠D.
(2)由(1)得,∠A=∠D
∴ AB//CD
∴ △OAE∽△ODF,△OBE∽△OCF
∴ \frac{AE}{FD}=\frac{AO}{OD},\frac{EB}{CF}=\frac{BO}{CO}
由(1)知∴ \frac{BO}{CO}=\frac{AO}{DO}
∴ \frac{AE}{FD}=\frac{EB}{CF}
∵ AE=BE
∴ CF=DF.
 初中数学应熟记数值表(平方、立方、2的n次方、常用分数值)
初中数学应熟记数值表(平方、立方、2的n次方、常用分数值) 《是妈妈是女儿》聚焦母女间未曾言明的爱意,以书信对话的形式呈现出各自的内心独白,表达彼此的牵挂。黄绮珊与希林娜依·高用跨越时空、打开心扉、深情对唱的形式,将天下母女爱的寄语化作心灵的倾诉。黄绮珊的每一句话,每一个字都演绎出了妈妈对女儿的爱,而希林依娜·高把女儿对妈妈的爱由不理解到理解再到感恩演绎得淋漓尽致。
《是妈妈是女儿》聚焦母女间未曾言明的爱意,以书信对话的形式呈现出各自的内心独白,表达彼此的牵挂。黄绮珊与希林娜依·高用跨越时空、打开心扉、深情对唱的形式,将天下母女爱的寄语化作心灵的倾诉。黄绮珊的每一句话,每一个字都演绎出了妈妈对女儿的爱,而希林依娜·高把女儿对妈妈的爱由不理解到理解再到感恩演绎得淋漓尽致。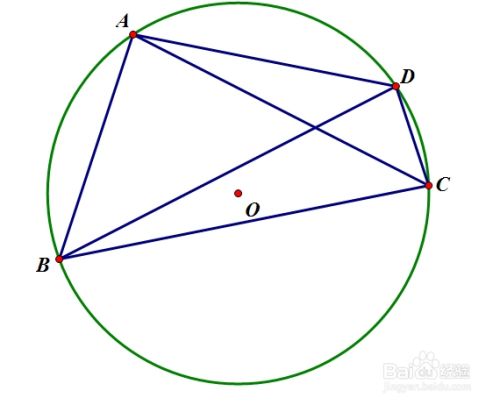 四点共圆:若在同一个平面内,有四个点在同一个圆上,则称这四个点共圆,一般简称“四点共圆”.
四点共圆:若在同一个平面内,有四个点在同一个圆上,则称这四个点共圆,一般简称“四点共圆”. 阿基米德(公元前287年—公元前212年),伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家,静态力学和流体静力学的奠基人,并且享有“力学之父”的美称,阿基米德和高斯、牛顿并列为世界三大数学家。阿基米德曾说过:“给我一个支点,我就能撬起整个地球。
阿基米德(公元前287年—公元前212年),伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家,静态力学和流体静力学的奠基人,并且享有“力学之父”的美称,阿基米德和高斯、牛顿并列为世界三大数学家。阿基米德曾说过:“给我一个支点,我就能撬起整个地球。 人教版数学九年级上册第二十三章《旋转》知识点,包含旋转的概念、性质、中心对称、中心对称图形的定义和性质、点关于原点对称等
人教版数学九年级上册第二十三章《旋转》知识点,包含旋转的概念、性质、中心对称、中心对称图形的定义和性质、点关于原点对称等 快速生成表格
快速生成表格 打包出现如下错误:Error: Application entry file "dist\electron\main.js" in the "D:\gui\demo2\build\win-unpacked\resources\app.asar" does not exist. Seems like a wrong configuration.
打包出现如下错误:Error: Application entry file "dist\electron\main.js" in the "D:\gui\demo2\build\win-unpacked\resources\app.asar" does not exist. Seems like a wrong configuration. Docker编译镜像出现:fetch http://dl-cdn.alpinelinux.org/alpine/v3.12/main/x86_64/APKINDEX.tar.gz
ERROR: http://dl-cdn.alpinelinux.org/alpine/v3.12/main: temporary error (try again later)
WARNING: Ignoring APKINDEX.2c4ac24e.tar.gz: No such file or directory问题
Docker编译镜像出现:fetch http://dl-cdn.alpinelinux.org/alpine/v3.12/main/x86_64/APKINDEX.tar.gz
ERROR: http://dl-cdn.alpinelinux.org/alpine/v3.12/main: temporary error (try again later)
WARNING: Ignoring APKINDEX.2c4ac24e.tar.gz: No such file or directory问题 在Mac电脑中,如何对Git的用户名和密码进行修改呢?起初不懂Mac,所以整了很久,本文将记录如何对这个进行操作,以便后期使用。
在Mac电脑中,如何对Git的用户名和密码进行修改呢?起初不懂Mac,所以整了很久,本文将记录如何对这个进行操作,以便后期使用。 在使用Git的过程中,不想每次都输入用户名和密码去拉取代码,所以就需要保存这些信息,那么既然有保存了,就必须有清除功能。
在使用Git的过程中,不想每次都输入用户名和密码去拉取代码,所以就需要保存这些信息,那么既然有保存了,就必须有清除功能。