一、算术平方根

1、算术平方根的定义：一般地，如果一个正数x的平方等于a，即x^2=a，那么这个正数x叫做a的算术平方根。

规定： 0的算术平方根是0.

2、算术平方根的表示方法： a的算术平方根记作\sqrt a，读作“根号a”，a叫做被开方数。

注意：
（1）算术平方根\sqrt a具有双重非负性；
a、被开方数a是非负数，即a≥0；
b、算术平方根\sqrt a是非负数，即\sqrt a≥0.
（2）算术平方根是它本身的数只有0和1.

3、算术平方根的性质
（1）正数的算术平方根是一个正数；
（2）0的算术平方根是0；
（3）负数没有算术平方根；
（4）被开方数越大，对应的算术平方根也越大。

二、算术平方根的估算

1、求一个正数（非平方数）的算术平方根的近似值，一般采用夹逼法.
“夹” 就是从两边确定取值范围；
“逼” 就是一点一点加强限制，使其所处范围越来越小，从而达到理想的精确程度。
2、采用计算器。

三、平方根

1、平方根的定义： 一般地，如果一个数的平方等于a，那么这个数叫做a的平方根或二次方根。这就是说：如果x^2=a，那么x叫做a的平方根。

2、平方根的表示方法： 非负数a的平方根记作±\sqrt a，读作“正、负根号a”，a叫做被开方数。

3、开平方： 求一个数a的平方根的运算，叫做开平方。

4、平方根的性质
（1）正数有两个平方根，它们互为相反数；
（2）0的平方根是0；
（3）负数没有平方根。

四、立方根的

1、立方根的定义：一般地，如果一个数的立方等于a，那么这个数叫做a的立方根或三次方根。也就是说，如果x^3=a，那么x叫做a的立方根.

2、立方根的表示方法：一个数a的立方根，用符号“\sqrt[3]{a}”，读作“三次根号a”，其中a是被开方数，3是根指数.

3、开立方：求一个数的立方根的运算，叫做开立方。开立方和立方互为逆运算.

4、立方根的性质
（1）正数的立方根是正数；
（2）负数的立方根是负数；
（3）0的立方根是0。
（4）一般地：\sqrt[3]{-a}=-\sqrt[3]{a}
\sqrt[3]{a^3}=a，(\sqrt[3]{a})^3=a，\sqrt[3]{a^3}=(\sqrt[3]{a})^3

五、无理数

1、无理数的定义：无限不循环小数叫做无理数；

2、判断标准：小数位无限，小数形式为不循环。

3、常见的无理数：
（1）开方开不尽的数，如\sqrt{3}，\sqrt[3]{5}，……
（2）含有\pi的一类数，如\frac{1}{3}\pi，\pi+1……
（3）以无限不循环小数的形式出现的特定结构的数，如：0.1010010001000001…

4、无理数与有理数的区别
（1）有理数是有限小数或无限循环小数，而无理数是无限不循环小数；
（2）所有的有理数都可以写成分数的形式（整数可以看成分母为1的分数），而无理数不能写成分数的形式.

六、实数

1、实数的定义：有理数和无理数通称实数.

注意：
（1）在实数范围内，一个数不是有理数，就一定是无理数，反之也成立；
（2）引入无理数后，数的范围就由原来的有理数扩大到了实数，今后没有严格说明时，就应该是在实数范围内.

2、实数的分类
（1）按定义分类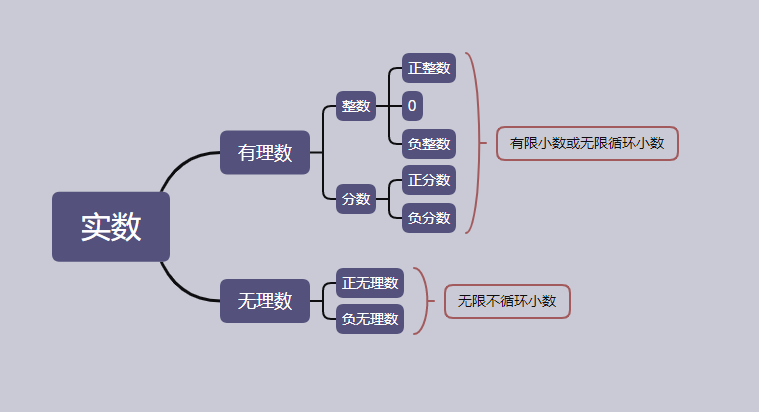

（2）按性质分类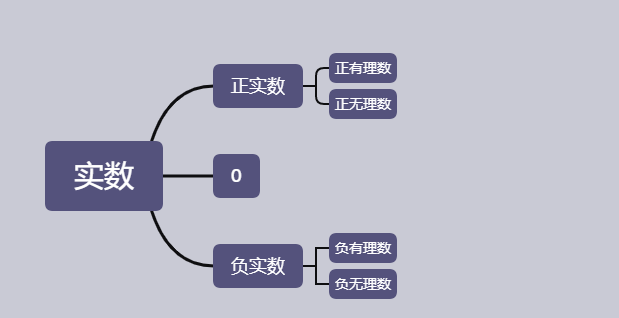

七、实数与数轴

1、实数与数轴间的关系：实数与数轴上的点是一一对应的.
(1)“一一对应”包含两层含义
a、每一个实数都可以用数轴上的一个点表示；
b、数轴上的每一个点都表示一个实数；
(2)数轴上的两个点之间的距离可以用两点所表示的实数来表示，即点A，点B在数轴上表示的数为x_1,x_2，则AB=|x_1-x_2|。

2、利用数轴比较实数的大小
对于数轴上任意两个点，右边的点表示的实数总比左边的点表示的实数大.

八、实数的性质

1、相反数：实数a的相反数为-a，若a，b互为相反数，则a+b=0；
2、倒数：非零实数a的倒数为\frac{1}{a}，若a,b互为倒数，则ab=1；
3、绝对值：
（1）|a|=a（a≥0）
（2）|a|=-a（a < 0）
4、实数比较大小：
（1）正数大于0,0大于一切负数；
（2）两个正数，绝对值大的数大，两个负数，绝对值大的数反而小.

九、实数的运算

实数的运算满足有理数运算的运算法则和运算律，如
加法交换律：a+b=b+a
加法结合律：(a+b)+c=a+(b+c)
乘法交换律：ab=ba
乘法结合律：(ab)c=a(bc)
乘法分配律：(a+b)c=ac+bc