RJ九上第二十二章《二次函数》知识点
一、二次函数
1、二次函数定义
一般地,形如y=ax^2+bx+c(a,b,c为常数,a≠0)的函数,叫做二次函数。其中x是自变量,a,b,c分别是函数解析式的二次项系、一次性系数和常数项。
2、确定二次函数的“三要素”
(1)含有自变量的代数式必须是整式;
(2)化简后自变量的最高次项次数是2;
(3)二次项系数不等于0.
3、运用定义法判断一个函数是否为二次函数的步骤:
(1)将函数解析式右边整理为含自变量的代数式,左边是函数(因变量)的形式;
(2)判断右边含自变量的代数式是否是整式;
(3)判断自变量的最高次数是否是2;
(4)判断二次项系数是否不等于0.
二、二次函数y = ax^2
(一)、二次函数y = ax^2的画法
1、抛物线
二次函数y = ax^2+bx+c的图象是一条曲线,这条曲线叫做抛物线y = ax^2+bx+c.
抛物线顶点:
抛物线是轴对称图形,抛物线与其对称轴的交点叫做抛物线的顶点,顶点是抛物线的最低点或最高点.
2、用描点法画函数y = ax^2(a≠0)的图象的一般步骤
(1)列表:
自变量x的取值应有一定的代表性,并且所对应的函数值不能太大也不能太小,以便描点和全面反映图象的情况.
(2)描点:
点取的越多、越密集,画出的图象就越准确.
(3)连线:
按自变量由小到大(或由大到小)的顺序,依次用平滑的曲线连接各点.
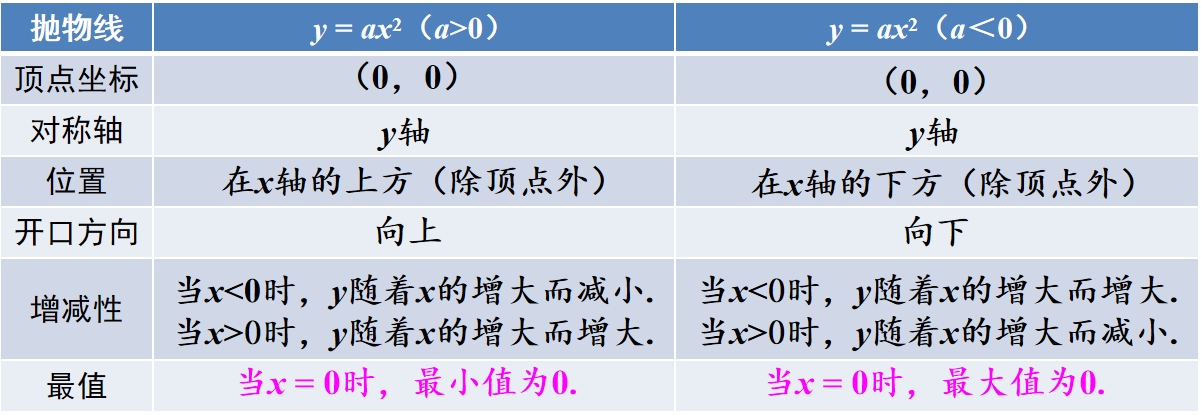
(二)、二次函数y = ax^2的图象和性质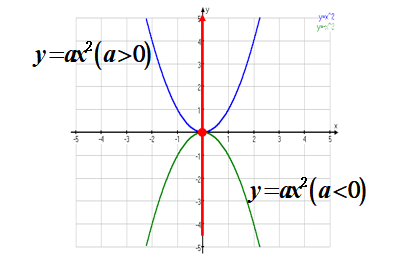
三、二次函数y=ax^2+k
(一)、二次函数y=ax^2+k的图象和性质
1、二次函数y=ax^2+k的图象与二次函数y=ax^2图象的关系
它们的开口大小、方向相同,只是上、下位置不同,二次函数y=ax^2+k的图象可由二次函数y=ax^2的图象上下平移|k|个单位长度得到.
2、二次函数y=ax^2+k的图象和性质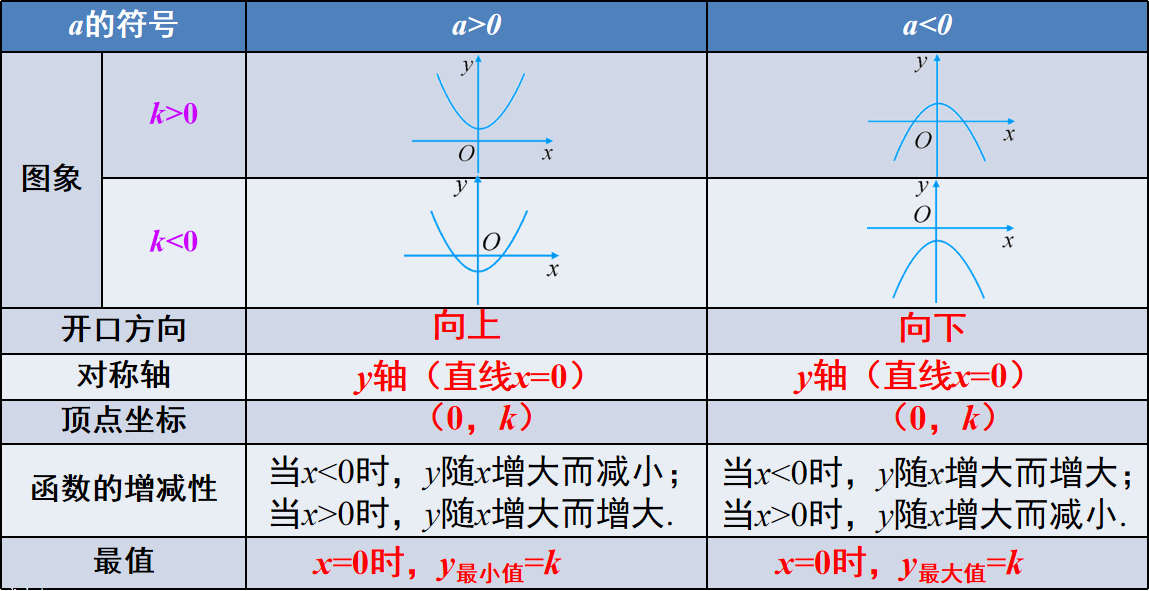
3、二次函数y=ax^2+k的图象的画法
(1)描点法:按列表→描点→连线的顺序作图;
(2)平移法:将二次函数y=ax^2的图象,向上(k>0)或向下(k\lt 0)平移|k|个单位长度,即可得到二次函数y=ax^2+k的图象.
(二)、二次函数y=a(x-h)^2的图象和性质
1、二次函数y=a(x-h)^2的图象与二次函数y=ax^2图象的关系
它们的开口大小、方向相同,只是左右位置不同,二次函数y=a(x-h)^2的图象可由二次函数y=ax^2的图象左右平移|k|个单位长度得到.
2、二次函数y=a(x-h)^2的图象和性质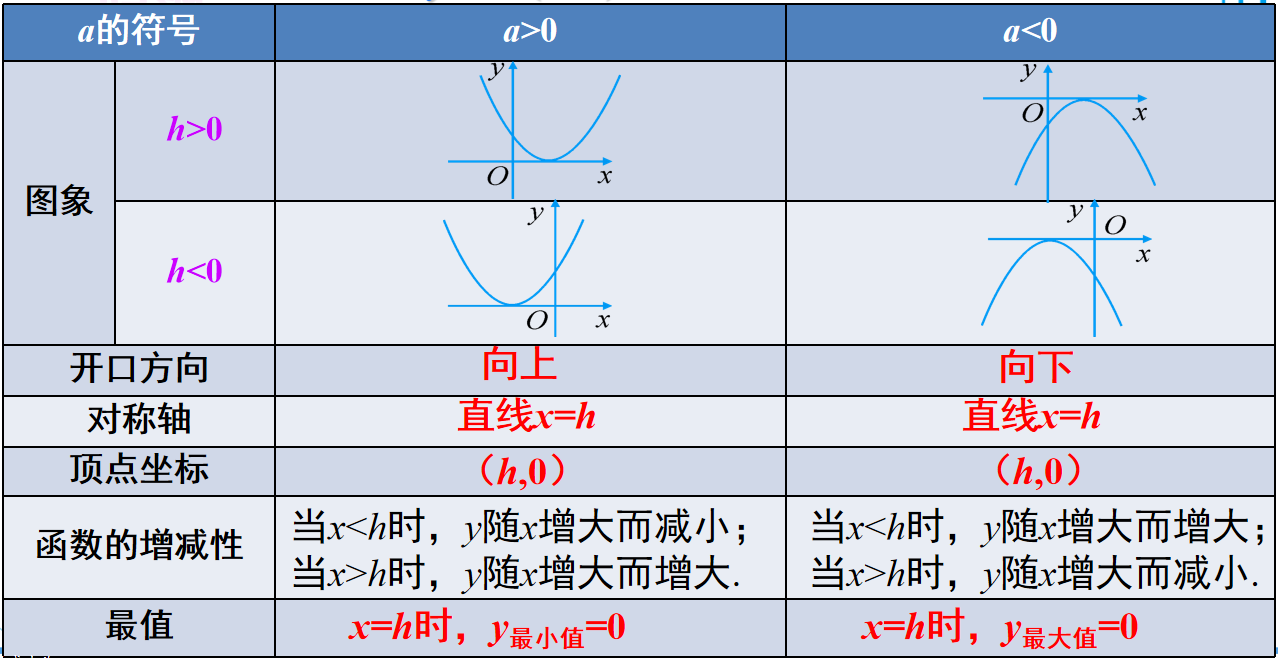
(三)、二次函数y=a(x-h)^2+k的图象和性质
1、二次函数y=a(x-h)^2+k的图象与二次函数y=ax^2图象的关系
它们的开口大小、方向相同,只是位置不同,二次函数y=a(x-h)^2+k的图象可由二次函数y=ax^2的图象平移得到.
2、二次函数y=a(x-h)^2+k的图象和性质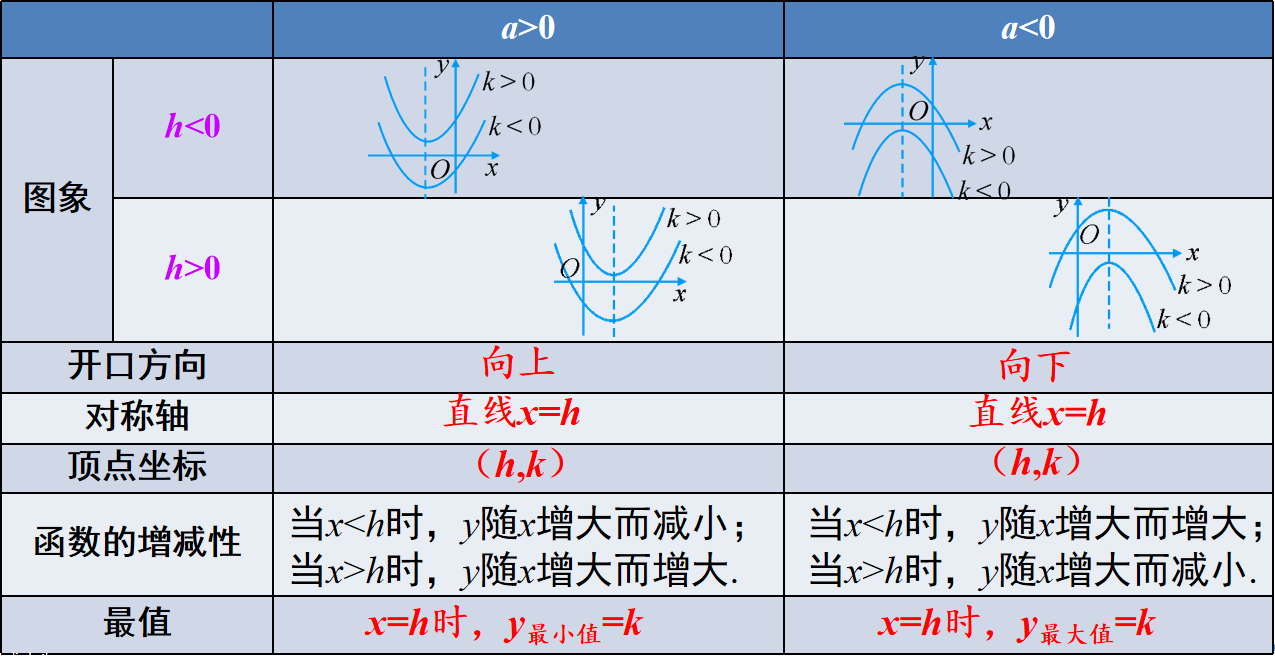
(四)、二次函数y=ax^2,y=ax^2+k,y=a(x-h)^2,y=a(x-h)^2+k之间的关系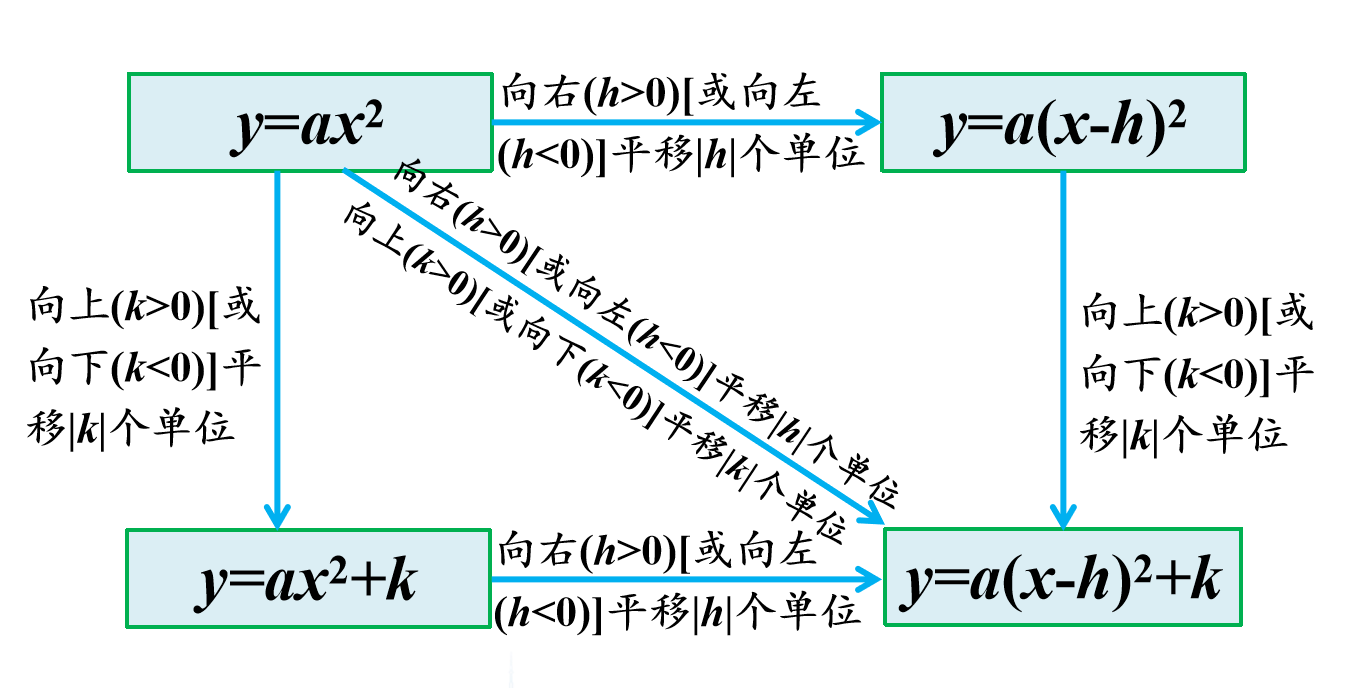
三、二次函数y=ax^2+bx+c
(一)、二次函数y=ax^2+bx+c与二次函数y=a(x-h)^2+k之间的关系
1、二次函数一般式y=ax^2+bx+c与二次函数顶点式y=a(x-h)^2+k的互化
y=ax^2+bx+c
=a(x^2+\frac{b}{a}x)+c
=a[x^2+\frac{b}{a}x+(\frac{b}{2a})^2-(\frac{b}{2a})^2]]+c
=a[(x+\frac{b}{a})^2-(\frac{b}{2a})^2]]+c
=a(x+\frac{b}{2a})^2-\frac{b^2}{4a}+c
=a(x+\frac{b}{2a})^2+\frac{4ac-b^2}{4a}
所以 h=-\frac{b}{2a},k=\frac{4ac-b^2}{4a}.
2、二次函数y=ax^2+bx+c的图象的画法
方法一:描点法
(1)把二次函数y=ax^2+bx+c化为y=a(x-h)^2+k的形式;
(2)确定抛物线的开口方向、对称轴和顶点坐标;
(3)在对称轴的两侧,已顶点为中心,左右对称描点并用光滑的曲线顺次连接.
方法二:平移法
(1)把二次函数y=ax^2+bx+c化为y=a(x-h)^2+k的形式;
(2)做出二次函数y=ax^2的图象;
(3)将二次函数y=ax^2的图象平移,使其顶点平移到(h,k)。
3、二次函数的对称性
对于二次函数y=ax^2+bx+c的图象上的两点P_1(x_1,y_1),P_2(x_2,y_2),若P_1(x_1,y_1)与P_2(x_2,y_2)关于直线x=-\frac{b}{2a}对称,则y_1=y_2,\frac{x_1+x_2}{2}=-\frac{b}{2a}.
(二)、二次函数y=ax^2+bx+c的图象和性质(与y=a(x-h)^2+k图象和性质)对比
(三)、用待定系数法求二次函数的解析式
1、常见的二次函数解析式的适用条件
(1)一般式y=ax^2+bx+c(a,b,c为常数,a≠0),当已知抛物线上三点的坐标时,可设一般式;
(2)顶点式y=a(x-h)^2+k(a,h,k为常数,a≠0),当已知抛物线的顶点坐标或对称轴或最大(小)值时,可设顶点式;
(3)交点式y=a(x-x_1)(x-x_2)(a,x_1,x_2为常数,a≠0),当已知抛物线与x轴的两个交点(x_1,0),(x_2,0)时,可以设交点式.
2、用待定系数法求二次函数解析式的步骤
(1)设:根据题中已知条件,合理设出二次函数的解析式;
(2)代:把已知点的坐标代入所设的二次函数的解析式中,得到关于解析式中待定系数的方程或方程组;
(3)解:解次方程或方程组,求出待定系数的值;
(4)还原:将求出的待定系数还原到解析式中,求得解析式.
3、特殊位置抛物线的解析式的设法
(1)顶点在原点,可设为y=ax^2;
(2)对称轴在y轴(或顶点在y轴上),可设为y=ax^2+k;
(3)顶点在x轴,可设为:y=a(x-h)^2;
(4)抛物线过原点,可设为y=ax^2+bx。
四、二次函数与一元二次方程的关系
1、二次函数图象与x轴的交点横坐标与一元二次方程根的关系
一般地,从二次函数y=ax^2+bx+c(a≠0)的图象可知:如果抛物线y=ax^2+bx+c(a≠0)与x轴有公共点,公共点的横坐标是x_0,那么当x=x_0时,函数值是0,因此x=x_0时方程ax^2+bx+c=0(a≠0)的一个根.
2、二次函数与一元二次方程的联系与区别
一元二次方程ax^2+bx+c=0(a≠0)与二次函数y=ax^2+bx+c(a≠0)二者之间的联系与区别,列表如下: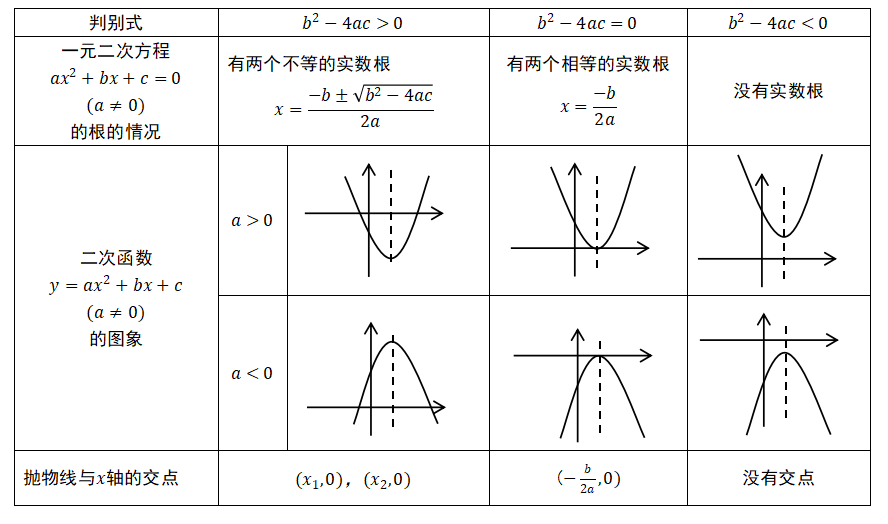
五、二次函数的图象与一元二次方程的近似解的关系
二次函数y=ax^2+bx+c(a≠0)的图象与x轴的公共点的横坐标是一元二次方程ax^2+bx+c=0(a≠0)的解,因此可以借助二次函数的图象求一元二次方程的解.
1、利用二次函数y=ax^2+bx+c(a≠0)的图象与x轴的公共点求一元二次方程ax^2+bx+c=0(a≠0)的解
(1)作出二次函数y=ax^2+bx+c(a≠0)的图象,确定图象与x轴公共点的个数,就是方程ax^2+bx+c=0(a≠0)的解的个数.
(2)观察图形,函数图象与x轴的交点的横坐标就是一元二次方程ax^2+bx+c=0(a≠0)的解,当函数图象与x轴有两个交点,且交点的横坐标不是整数时,可以通过缩小解所在的范围估计一元二次方程的解.
2、利用二次函数y=ax^2的图象与直线y=-bx-c的公共点求方程ax^2+bx+c=0(a≠0)的解
(1)将方程ax^2+bx+c=0(a≠0)化为ax^2=-bx-c的形式;
(2)在平面直角坐标系中画出抛物线y=ax^2和直线y=-bx-c,并确定抛物线与直线公共点的坐标;
(3)公共点的横坐标即为一元二次方程ax^2+bx+c=0(a≠0)的解。
六、二次函数y=ax^2+bx+c的图象的特征与a,b,c的符号关系
二次函数y=ax^2+bx+c(a≠0)中,a的符号决定抛物线的开口方向,ab的符号决定抛物线的对称轴的大致位置,c的符号决定抛物线与y轴的大致位置,b^2-4ac的符号决定抛物线与x轴的交点情况.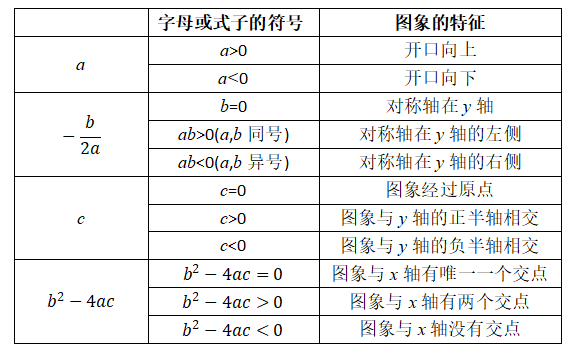
 相似三角形是初中几何中非常重要的内容,常常与其他知识点结合,是中考的常考题型。本节主要介绍相似三角形模型——A字型和8字型模型
相似三角形是初中几何中非常重要的内容,常常与其他知识点结合,是中考的常考题型。本节主要介绍相似三角形模型——A字型和8字型模型 Towxml 是一个让小程序(微信/QQ)可以解析Markdown、HTML的解析库。能够使小程序完美解析Markdown内容。
Towxml 是一个让小程序(微信/QQ)可以解析Markdown、HTML的解析库。能够使小程序完美解析Markdown内容。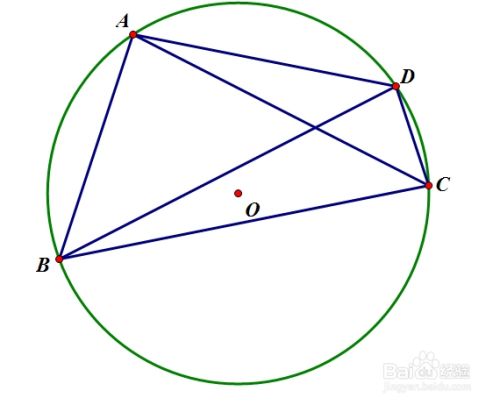 四点共圆:若在同一个平面内,有四个点在同一个圆上,则称这四个点共圆,一般简称“四点共圆”.
四点共圆:若在同一个平面内,有四个点在同一个圆上,则称这四个点共圆,一般简称“四点共圆”. 人教版数学九年级下册第二十六章《反比例函数》知识点,包含反比例函数的概念、图象和性质、反比例函数的实际应用等
人教版数学九年级下册第二十六章《反比例函数》知识点,包含反比例函数的概念、图象和性质、反比例函数的实际应用等 默认情况下 pip 使用的是国外的镜像,在下载的时候速度非常慢,本文我们介绍使用国内源对pip进行加速。
默认情况下 pip 使用的是国外的镜像,在下载的时候速度非常慢,本文我们介绍使用国内源对pip进行加速。 快速生成表格
快速生成表格 打包出现如下错误:Error: Application entry file "dist\electron\main.js" in the "D:\gui\demo2\build\win-unpacked\resources\app.asar" does not exist. Seems like a wrong configuration.
打包出现如下错误:Error: Application entry file "dist\electron\main.js" in the "D:\gui\demo2\build\win-unpacked\resources\app.asar" does not exist. Seems like a wrong configuration. Docker编译镜像出现:fetch http://dl-cdn.alpinelinux.org/alpine/v3.12/main/x86_64/APKINDEX.tar.gz
ERROR: http://dl-cdn.alpinelinux.org/alpine/v3.12/main: temporary error (try again later)
WARNING: Ignoring APKINDEX.2c4ac24e.tar.gz: No such file or directory问题
Docker编译镜像出现:fetch http://dl-cdn.alpinelinux.org/alpine/v3.12/main/x86_64/APKINDEX.tar.gz
ERROR: http://dl-cdn.alpinelinux.org/alpine/v3.12/main: temporary error (try again later)
WARNING: Ignoring APKINDEX.2c4ac24e.tar.gz: No such file or directory问题 在Mac电脑中,如何对Git的用户名和密码进行修改呢?起初不懂Mac,所以整了很久,本文将记录如何对这个进行操作,以便后期使用。
在Mac电脑中,如何对Git的用户名和密码进行修改呢?起初不懂Mac,所以整了很久,本文将记录如何对这个进行操作,以便后期使用。 在使用Git的过程中,不想每次都输入用户名和密码去拉取代码,所以就需要保存这些信息,那么既然有保存了,就必须有清除功能。
在使用Git的过程中,不想每次都输入用户名和密码去拉取代码,所以就需要保存这些信息,那么既然有保存了,就必须有清除功能。