RJ九上第二十三章《旋转》知识点
一、旋转
1.1、旋转及其相关概念
1、定义:把一个平面图形绕着平面内某一点O转动一个角度,叫做图形的旋转。点O叫做旋转中心,转动的角度叫做旋转角.
2、旋转的“三要素”:旋转中心、旋转方向和旋转角。
(1)在旋转的过程中,旋转中心可以在图形的内部,也可在图形的外部,也可以是图形上的某点;
(2)旋转方向有顺时针和逆时针两种.
3、对应元素
旋转得到的图形能与原图形重合,我们把能够重合的点叫做对应点,能够重合的线段叫做对应线段,能够重合角叫做对应角。
2.1、旋转的性质
1、对应点到旋转中心的距离相等;
2、对应点与旋转中所连线段的夹角等于旋转角;
3、旋转前、后的图形全等.
提醒:旋转中心是两对对应点所连线段垂直平分线的交点。
3.1、旋转作图
1、作图依据:旋转的性质,即对应点到旋转中心的距离相等,每组对应点都旋转了相同的角度.
2、旋转作图的一般步骤:
(1)确定旋转中心、旋转方向和旋转角;
(2)找出图形的关键点,一般是图形中的转折点;
(3)作旋转后的对应点,方法如下:
a、连:链接图象的每个关键点与旋转中心;
b、转:把连线绕旋转中心按旋转方向旋转相同角度;
c、截:在作得的角的另一边截取与关键点到旋转中心的距离相等的线段,得到各个关键点的对应点
(4)按原图的顺序连接这些对应点,所得到的图形就是旋转后的图形;
(5)写出结论,说明做出的图形即为所作的图形.
二、中心对称
2.1、中心对称相关概念
1、定义:把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心。这两个图形在旋转后能够重合的对应点叫做关于对称中心的对称点.
2、中心对称与轴对称的关系
2.2、中心对称性质
1、性质
(1)中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分;反之,如果两个图形的对应点的连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点中心对称,利用这一性质可以识别中心对称;
(2)中心对称的两个图形是全等图形,对应角相等,对应线段平行(或在同一直线上)且相等.
2、确定对称中心的方法
方法一:连接任意一对对称点,确这条线段的中点,则该中点为对称中心;
方法二:任意连接两对对称点,这两条线段的交点就是对称中心.
3、性质延伸
(1)对称中心在一对对称点的连线上;
(2)对称中心到一对对称点的距离相等.
4、全等的图形不一定成中心对称,而成中心对称的两个图形一定是全等的图形.
2.3、中心对称作图
1、作图关键
确定对称中心,再作出原图上关键点关于对称中心的对称点.
2、作图步骤
(1)分别将原图形上的所有关键点与对称中心连接;
(2)将以上连接延长线找对称点,使得对称点与对称中心的距离和关键点与对称中心的距离相等;
(3)将对称点按原图形的形状顺次连接起来,即可得出关于对称中心对称的图形.
三、中心对称图形
3.1、中心对称图形的定义
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
3.2、中心对称图形的性质
1、中心对称图形上的对称点的连线必经过对称中心,且被对称中心平分,即过对称中心的直线与中心对称图形所交的两个点是对称点;中心对称图形上所有的点关于对称中心的对称点都在这个图形上.
2、过对称中心的任意一条直线把中心对称图形分成了全等的两个部分.
3.3、中心对称与中心对称图形的区别和联系
1、区别:
中心对称:
(1)针对的是两个图形而言;
(2)是指两个图形的位置关系;
(3)对称点在两个图形上;
中心对称图形:
(1)针对一个图形而言;
(2)是指具有某种性质的一个图形;
(3)对称点在一个图形上.
2、联系
(1)若把中心对称的两个图形视为一个整体,则整个图形是中心对称图形;
(2)若把中心对称图形互相对称的两个部分看作是两个图形,则这两个图形成中心对称.
3.4、常见的中心对称图形
线段、平行四边形、矩形、菱形、边数为偶数的正多边形、圆等
四、关于原点对称点的坐标
1、关于原点对称的点的坐标
两个点关于原点对称时,它们的横、纵坐标分别互为相反数,即点P(x,y)关于原点的对称点的坐标P′(-x,-y).
2、关于坐标轴对称和关于原点对称的点的坐标的区别
(1)关于x轴对称
横坐标相同,纵坐标互为相反数,即P(a,b)关于x轴对称的对称点P′(a,-b)
(2)关于y轴对称
横坐标互为相反数,纵坐标相同,即P(a,b)关于x轴对称的对称点P′(-a,b)
(3)关于原点对称
横、纵坐标互为相反数,即P(a,b)关于原点的对称点的坐标P′(-a,-b).
 在使用Git的过程中,不想每次都输入用户名和密码去拉取代码,所以就需要保存这些信息,那么既然有保存了,就必须有清除功能。
在使用Git的过程中,不想每次都输入用户名和密码去拉取代码,所以就需要保存这些信息,那么既然有保存了,就必须有清除功能。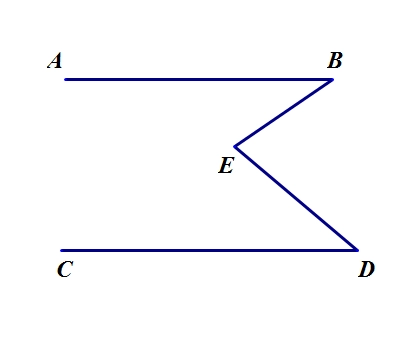 由于这中模型看起来长得像“猪蹄”,所以就把它叫做猪蹄模型,当然也有叫锯齿模型、M模型。本文主要介绍猪蹄模型.
由于这中模型看起来长得像“猪蹄”,所以就把它叫做猪蹄模型,当然也有叫锯齿模型、M模型。本文主要介绍猪蹄模型. iostat是I/O statistics的缩写,起主要功能是对系统的磁盘I/O操作进行监控。他的输出主要是显示磁盘的读写操作的统计信息,同时也会给出CPU的使用情况。iostat命令也只能对系统的整体情况进行分析,不能对某个进程进行分析。
iostat是I/O statistics的缩写,起主要功能是对系统的磁盘I/O操作进行监控。他的输出主要是显示磁盘的读写操作的统计信息,同时也会给出CPU的使用情况。iostat命令也只能对系统的整体情况进行分析,不能对某个进程进行分析。 APM(Application Performance Management)即应用性能管理系统,是对企业系统及时监控以实现对应用程序性能管理和故障管理的系统化解决方案。应用性能管理,主要指对企业的关键业务应用进行监控、优化,提高企业的应用的可靠性和治理,保证用户得到良好的服务,减低IT总拥有成本。
APM(Application Performance Management)即应用性能管理系统,是对企业系统及时监控以实现对应用程序性能管理和故障管理的系统化解决方案。应用性能管理,主要指对企业的关键业务应用进行监控、优化,提高企业的应用的可靠性和治理,保证用户得到良好的服务,减低IT总拥有成本。 初中数学:平面直角坐标系中三角形面积求法
初中数学:平面直角坐标系中三角形面积求法 快速生成表格
快速生成表格 打包出现如下错误:Error: Application entry file "dist\electron\main.js" in the "D:\gui\demo2\build\win-unpacked\resources\app.asar" does not exist. Seems like a wrong configuration.
打包出现如下错误:Error: Application entry file "dist\electron\main.js" in the "D:\gui\demo2\build\win-unpacked\resources\app.asar" does not exist. Seems like a wrong configuration. 在Mac电脑中,如何对Git的用户名和密码进行修改呢?起初不懂Mac,所以整了很久,本文将记录如何对这个进行操作,以便后期使用。
在Mac电脑中,如何对Git的用户名和密码进行修改呢?起初不懂Mac,所以整了很久,本文将记录如何对这个进行操作,以便后期使用。 Docker编译镜像出现:fetch http://dl-cdn.alpinelinux.org/alpine/v3.12/main/x86_64/APKINDEX.tar.gz
ERROR: http://dl-cdn.alpinelinux.org/alpine/v3.12/main: temporary error (try again later)
WARNING: Ignoring APKINDEX.2c4ac24e.tar.gz: No such file or directory问题
Docker编译镜像出现:fetch http://dl-cdn.alpinelinux.org/alpine/v3.12/main/x86_64/APKINDEX.tar.gz
ERROR: http://dl-cdn.alpinelinux.org/alpine/v3.12/main: temporary error (try again later)
WARNING: Ignoring APKINDEX.2c4ac24e.tar.gz: No such file or directory问题