【代数法】存在性问题之等腰三角形
相比几何方法求解等腰三角形存在性问题,代数方法显得就比较简单直接。最重要的公式就是,两点间距离公式。
一、两点间距离公式
设两个点A、B以及坐标分别为(x_1,y_1)、 (x_2,y_2),则A和B两点之间的距离为:
|AB|=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}
二、例题讲解
下面我们就以前面的一道例题来进行说明: 解: 由题意得,B、C点坐标分别为(3,0),(0,3),设P点坐标为(1,m),则: 例2、 如图,抛物线y=ax^2+bx+4交x轴于A(-3,0),B(4,0)两点,与y轴交于点C,连接AC,BC.点P是第一象限内抛物线上的一个动点,点P的横坐标为m. 1、先计算出三角形每边的距离,采用两点间距离公式,通常用平方表示;
例、 如图,已知抛物线解析式为y=-x^2+2x+3,与x轴交于A、B两点,与y轴交于点C。在抛物线对称轴上是否存在一点P,使得△PCB为等腰三角形?若存在,请求出符合条件的P点坐标;若不存在说明理由?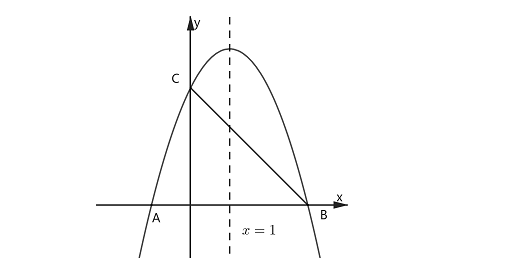
分析: 根据题意我们可以求出B、C点坐标,分别为(3,0),(0,3),
P点是抛物线对称轴上一动点,所以需要先设P点坐标,既然P点在x=1这条直线上,所以横坐标为1,则设P点坐标为(1,m),
分别计算BC、PC、PB的长度,使用两点间距离公式,但是一般我们使用平方来表示,即:
BC^2=(0-3)^2+(3-0)^2=18
PC^2=(1-0)^2+(m-3)^2=m^2-6m+10
PB^2=(1-3)^2+(m-0)^2=m^2+4
下面分别以不同的点为顶点进行分类讨论:
① 当PB=PC时(以P点为顶点),则:
m^2+4=m^2-6m+10;
② 当BC=PB时(以B点为顶点),则:
18=m^2+4;
③ 当BC=PC时(以C点为顶点),则:
18=m^2-6m+10;
计算上面三种情况下m的值,但是还需要进行检验,可能求出的P点刚好与B、C共线呢?所以还需要求出BC所在直线的解析式,将上面的点代入到解析式中进行验证即可。
BC^2=(0-3)^2+(3-0)^2=18
PC^2=(1-0)^2+(m-3)^2=m^2-6m+10
PB^2=(1-3)^2+(m-0)^2=m^2+4
(1)当PB=PC时,即:
m^2+4=m^2-6m+10
解得:m=1
∴ P(1,1)
(2)当BC=PB时,即:
18=m^2+4
解得:m=±\sqrt{14}
∴ P(1,\sqrt{14})或P(1,-\sqrt{14})
(3)当BC=PC时,即:
18=m^2-6m+10
解得:m=3±\sqrt{17}
∴ P(1,3+\sqrt{17})或P(1,3-\sqrt{17})
∵ B、C点坐标分别为(3,0),(0,3)
∴ BC所在直线的解析式为:y=-x+3
∴ 经检验,以上各点都不在直线BC上
综上所述:满足△BCP是等腰三角形的P点坐标为:(1,1)、(1,\sqrt{14})、(1,-\sqrt{14})、(1,3+\sqrt{17})、(1,3-\sqrt{17}).
(1)求此抛物线的表达式;
(2)过点P作PM⊥x轴,垂足为点M,PM交BC于点Q.试探究点P在运动过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请求出此时点Q的坐标,若不存在,请说明理由;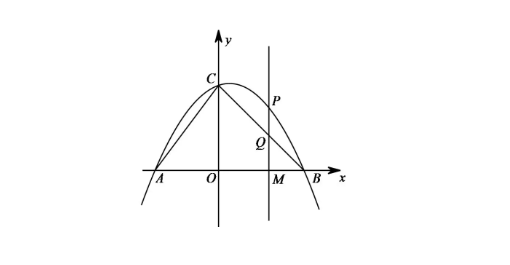
分析: 本题中A、C都是定点,P是抛物线第一象限内的一动点,则Q点也是一动点,且在线段BC(不含B、C两点)上运动,所以本题需要先求出BC所在直线的解析式,然后根据等腰三角形存在性问题代数法求解即可。
解: (1)将(-3,0),(4,0)代入抛物解析式得:
\left\{\begin{matrix} 9a-3b+4=0 \\ 16a+4b+4=0 \end{matrix} \right.
解得:\left\{\begin{matrix} a=-\frac{1}{3} \\ b=\frac{1}{3} \end{matrix} \right.
所以抛物线的解析式为:y=-\frac{1}{3}x^2+\frac{1}{3}x+4.
(2)∵ 抛物线的解析式为:y=-\frac{1}{3}x^2+\frac{1}{3}x+4
∴ C点坐标为(0,4)
∵ C(0,4),B(4,0)
∴ BC所在直线解析式为:
y=-x+4
Q点是直线CB上一动点,设Q点坐标为
(m,-m+4)
∵ A(-3,0),C(0,4)
∴ AC^2=25,
CQ^2=m^2+(-m+4-4)^2=2m^2,
AQ^2=(m+3)^2+(-m+4)^2=2m^2-2m+25
(1)当AC=AQ时,即:
25=2m^2-2m+25
解得:m=0(舍去)或m=1
∴ P(1,3)
(2)当AC=CQ时,即:
25=2m^2
解得:m=\frac{5\sqrt{2}}{2}或m=-\frac{5\sqrt{2}}{2}(舍去)
∴ P(\frac{5\sqrt{2}}{2},4-\frac{5\sqrt{2}}{2})
(3)当AQ=CQ时,即:
2m^2=2m^2-2m+15
解得:m=\frac{15}{2}(舍去)
综上所述:满足△ACQ是等腰三角形的Q点坐标为:(1,3)、(\frac{5\sqrt{2}}{2},4-\frac{5\sqrt{2}}{2}).三、使用代数法步骤
2、以各点为顶点,分类讨论腰相等三种情况,建立方程并求解;
3、检验所求点是否符合题意,不符合则舍去。
 我们在日常的学习中很多时候求三角形的面积都是通过定义法:底乘高的一半来计算,其实三角形的面积求法有多种,本文就主要介绍初中生应该掌握的多种求三角形面积的方法.
我们在日常的学习中很多时候求三角形的面积都是通过定义法:底乘高的一半来计算,其实三角形的面积求法有多种,本文就主要介绍初中生应该掌握的多种求三角形面积的方法. 初中数学:平面直角坐标系中四边形面积求法
初中数学:平面直角坐标系中四边形面积求法 初中数学:平面直角坐标系中三角形面积求法
初中数学:平面直角坐标系中三角形面积求法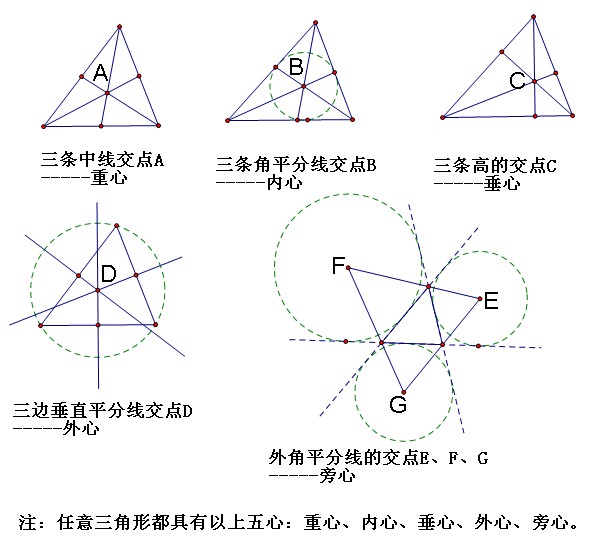 中学数学常用到的三角形的“心”有五个:内心、外心、重心、垂心、旁心。三角形的这五个“心”所涉及到的重要知识点如下。
中学数学常用到的三角形的“心”有五个:内心、外心、重心、垂心、旁心。三角形的这五个“心”所涉及到的重要知识点如下。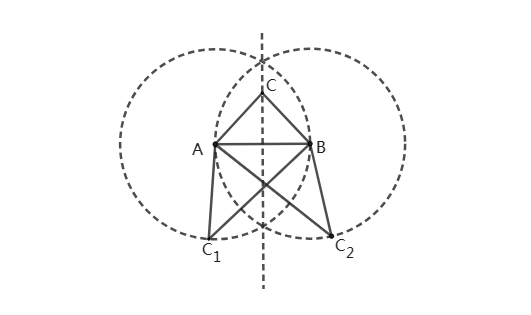 等腰三角形存在性问题在中考出现的频率比较高,那么我们可以通过几何的方式“两圆一线”来解决等腰三角形存在性问题。
等腰三角形存在性问题在中考出现的频率比较高,那么我们可以通过几何的方式“两圆一线”来解决等腰三角形存在性问题。 快速生成表格
快速生成表格 打包出现如下错误:Error: Application entry file "dist\electron\main.js" in the "D:\gui\demo2\build\win-unpacked\resources\app.asar" does not exist. Seems like a wrong configuration.
打包出现如下错误:Error: Application entry file "dist\electron\main.js" in the "D:\gui\demo2\build\win-unpacked\resources\app.asar" does not exist. Seems like a wrong configuration. 在Mac电脑中,如何对Git的用户名和密码进行修改呢?起初不懂Mac,所以整了很久,本文将记录如何对这个进行操作,以便后期使用。
在Mac电脑中,如何对Git的用户名和密码进行修改呢?起初不懂Mac,所以整了很久,本文将记录如何对这个进行操作,以便后期使用。 Docker编译镜像出现:fetch http://dl-cdn.alpinelinux.org/alpine/v3.12/main/x86_64/APKINDEX.tar.gz
ERROR: http://dl-cdn.alpinelinux.org/alpine/v3.12/main: temporary error (try again later)
WARNING: Ignoring APKINDEX.2c4ac24e.tar.gz: No such file or directory问题
Docker编译镜像出现:fetch http://dl-cdn.alpinelinux.org/alpine/v3.12/main/x86_64/APKINDEX.tar.gz
ERROR: http://dl-cdn.alpinelinux.org/alpine/v3.12/main: temporary error (try again later)
WARNING: Ignoring APKINDEX.2c4ac24e.tar.gz: No such file or directory问题 在使用Git的过程中,不想每次都输入用户名和密码去拉取代码,所以就需要保存这些信息,那么既然有保存了,就必须有清除功能。
在使用Git的过程中,不想每次都输入用户名和密码去拉取代码,所以就需要保存这些信息,那么既然有保存了,就必须有清除功能。