RJ九下第二十七章《相似》知识点
一、相似图形
1、定义:形状相同的图形叫做相似图形。
2、注意
(1)两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到;
(2)全等图形是特殊的相似图形,即全等图形一定是相似图形,但相似图形不一定是全等图形。
二、比例线段
1、线段的比:在同一长度单位下,量得的两条线段长度的比叫做这两条线段的比。
2、比例线段:对于四条线段a,b,c,d,如果其中两条线段的比(即它们长度的比)与另两条线段的比相等,如: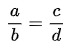 (即:ad=bc),我们就说这四条线段成比例。
(即:ad=bc),我们就说这四条线段成比例。
3、比例的相关性质
(1)比例基本性质的逆用:若ad=bc(bd≠0),则: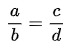 ;
;
(2)比例其他性质
a、反比、更比性质: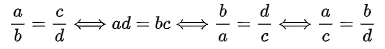
b、合比、分比性质: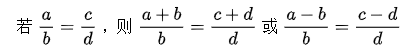
c、等比性质: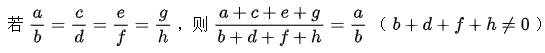
(3)黄金分割:如果点C把线段AB分成两条线段AC和BC(AC>BC),且AB:AC=AC:BC,叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点。
三、相似多边形
1、相似多边形:两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形。
2、相似比:相似多边形对应边的比叫做相似比。
3、相似多边形的性质:相似多边形的对应角相等,对应边成比例.
四、平行线分线段成比例定理
1、基本事实:两条直线被一组平行线所截,所得的对应线段成比例。
2、推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例。
五、相似三角形
1、定义:三个角分别相等,三条边成比例的两个三角形叫做相似三角形。
2、注意
(1)用符号“∽”表示两个三角形相似,表示两个三角形相似时,对应顶点的大写字母要对应上;
(2)如果仅说△ABC与△A'B'C'相似,没有用“∽”,则需要进行分类讨论它们之间的对应关系;
(3)相似三角形的相似比具有顺序性,即如果△ABC与△A'B'C'的相似比为k,那么△A'B'C'与△ABC的相似比为
六、相似三角形的判断定理
1、平行定理:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似;
2、三边定理:三边成比例的两个三角形相似。
3、两边及夹角定理:两边成比例且夹角相等的两个三角形相似。
4、两角定理:两角分别相等的两个三角形相似。
5、直角三角形相似的判定
斜边和一条直角边成比例的两个直角三角形相似。一个锐角相等的的两个直角三角形相似。
七、相似三角形的性质
1、相似三角形对应线段及周长的性质
(1)相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比,即相似三角形对应线段的比等于相似比。
(2)相似三角形的周长的比等于相似比。
2、相似三角形的面积的性质
相似三角形面积的比等于相似比的平方。
八、位似图形的概念
1、位似图形:两个图形不仅相似,而且对应顶点的连线相交于一点,像这样的两个图形叫做位似图形,这点叫做位似中心。
2、位似图形必须满足两个条件:
① 两个图形是相似图形;
② 两个相似图形的对应顶点的连线相交于一点。
3、位似多边形:对应两个多边形,如果它们的对应顶点的连线相交于一点,并且这点与对应顶点所连线段成比例,那么这两个多边形就是位似多边形。
4、位似图形的性质
(1)对应角相等,对应边成比例;
(2)位似图形的对应点的连线交于一点,即位似中心;
(3)位似图形的任意一对对应点到位似中心的距离之比都等于相似比;
(4)位似图形的对应线段平行(或在同一条直线上)且线段比等于相似比。
九、位似图形的画法
1、定:确定位似中心;
2、作:分别过位似中心和原图的各关键点作直线;
3、找:根据相似比,找出所作位似图形的对应点;
4、连:按原图连接各对应点,得到放大或缩小的图形。
十、平面直角坐标系中的位似变换
一般地,在平面直角坐标系中,如果以原点为位似中心,画出一个与原图形位似的图形,使它与原图形的相似比为k,那么原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或(-kx,-ky).
注意:求位似图形对应点的坐标时,要注意位似图形可以在位似中心的同侧,也可以在位似中心的两侧,需要根据题意分情况讨论。
十一、图形变换
1、位似、平移、轴对称、旋转都是图形变换的基本形式;
2、图形变换的种类:
(1)全等变换:不改变图形的大小和形状,包括平移、旋转、轴对称;
(2)位似变换:改变大小(扩大、缩小),不改变形状。
 nodejs中使用npm和yarn,使用最新阿里云镜像 aliyun mirror,网上很多还是文章用的是下面这个地址~~yarn config set registry https://registry.npm.taobao.org~~
nodejs中使用npm和yarn,使用最新阿里云镜像 aliyun mirror,网上很多还是文章用的是下面这个地址~~yarn config set registry https://registry.npm.taobao.org~~ 初中数学:平面直角坐标系中四边形面积求法
初中数学:平面直角坐标系中四边形面积求法 初中数学:平面直角坐标系中三角形面积求法
初中数学:平面直角坐标系中三角形面积求法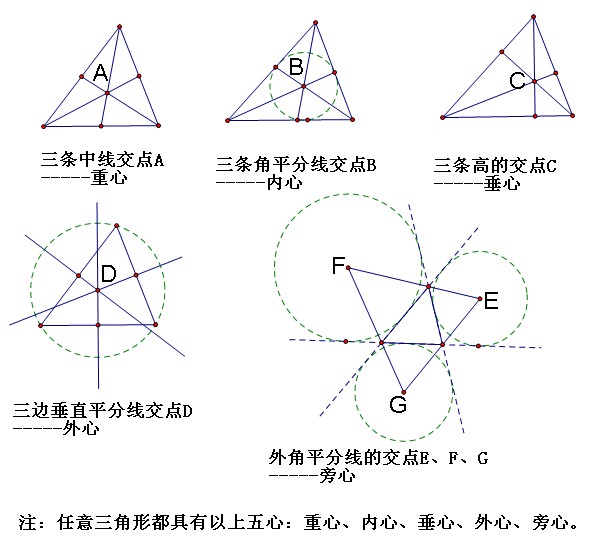 中学数学常用到的三角形的“心”有五个:内心、外心、重心、垂心、旁心。三角形的这五个“心”所涉及到的重要知识点如下。
中学数学常用到的三角形的“心”有五个:内心、外心、重心、垂心、旁心。三角形的这五个“心”所涉及到的重要知识点如下。 初中数学:一次函数补充知识点
初中数学:一次函数补充知识点 快速生成表格
快速生成表格 打包出现如下错误:Error: Application entry file "dist\electron\main.js" in the "D:\gui\demo2\build\win-unpacked\resources\app.asar" does not exist. Seems like a wrong configuration.
打包出现如下错误:Error: Application entry file "dist\electron\main.js" in the "D:\gui\demo2\build\win-unpacked\resources\app.asar" does not exist. Seems like a wrong configuration. 在Mac电脑中,如何对Git的用户名和密码进行修改呢?起初不懂Mac,所以整了很久,本文将记录如何对这个进行操作,以便后期使用。
在Mac电脑中,如何对Git的用户名和密码进行修改呢?起初不懂Mac,所以整了很久,本文将记录如何对这个进行操作,以便后期使用。 Docker编译镜像出现:fetch http://dl-cdn.alpinelinux.org/alpine/v3.12/main/x86_64/APKINDEX.tar.gz
ERROR: http://dl-cdn.alpinelinux.org/alpine/v3.12/main: temporary error (try again later)
WARNING: Ignoring APKINDEX.2c4ac24e.tar.gz: No such file or directory问题
Docker编译镜像出现:fetch http://dl-cdn.alpinelinux.org/alpine/v3.12/main/x86_64/APKINDEX.tar.gz
ERROR: http://dl-cdn.alpinelinux.org/alpine/v3.12/main: temporary error (try again later)
WARNING: Ignoring APKINDEX.2c4ac24e.tar.gz: No such file or directory问题 在使用Git的过程中,不想每次都输入用户名和密码去拉取代码,所以就需要保存这些信息,那么既然有保存了,就必须有清除功能。
在使用Git的过程中,不想每次都输入用户名和密码去拉取代码,所以就需要保存这些信息,那么既然有保存了,就必须有清除功能。