初中数学:二次函数之直角三角形存在性问题分析
二次函数是中考的必考考点,综合性非常强。本文主要介绍下二次函数中存在性问题的直角三角形存在性问题,其实这类题如果掌握好了方法,还是非常比较简单,很容易得到分。下面我们就利用例题对这类题型进行分析。
例、如图,在平面直角坐标系中,抛物线
(1)分别求直线BC和抛物线的解析式(关系式);
(2)在抛物线的对称轴上是否存在点P,使得以B,C,P三点为顶点的三角形是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.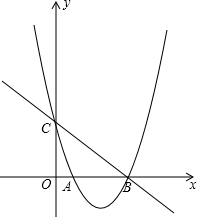
分析:这里二次函数题的第一问还是非常简单,第二问就是我们今天需要讨论的问题。点P是在抛物线的对称轴上,那么就需要先求对称轴是多少,这里我直接给出,对称轴为
要使得B,C,P三点为顶点的三角形是直角三角形,那么还需要求出B,C的坐标,这里也直接给出B(4,0),C(0,3).
以上我们把本题的需要的基本数据准备好了,下面我们开始分析如何构成直角三角形。
要使得B,C,P三点为顶点的三角形是直角三角形,那么并没有明确是以那个角为直角的直角三角形,那么这里需要干什么呢?
肯定需要“分类讨论”,分别讨论∠PCB=90°,∠PBC=90°,∠BPC=90°,这三种情况都需要讨论。
我们知道要进行分类讨论,那么如何来找出关系来求出P点坐标呢?这里就需要大家开动脑筋,把学过的知识点想一想,有哪些知识点是与直角或垂直有关呢?
1、首先,勾股定理,如果三角形是直角三角形,则三边满足a2+b2=c2。
2、其次,前面我们讲过两直线垂直,那么它们k的乘积为-1;
3、最后,也是大部分同学最不容易想到的,一线三垂直关系,既然这里需要直角,那么我们将一个角看成直角,去构造一线三垂直模型,利用相似三角形构造等量关系,即可解题。
一、利用勾股定理
如果利用勾股定理解题,就需要求出三边的长度,在平面直角坐标系中,求两点的距离公式就特别重要了,如果有两点
但是我们解这类题的时候,就直接写成距离的平方的形式:
那么我们根据B、C、P三点的坐标利用上面的公式分别表示出BC2,BP2,CP2,下一步就利用分类讨论,分别讨论即可。
二、利用直线斜率(k)
如果利用直线斜率(k),来解题,那么就需要先把三角形的三边都看着在直线上,那么就把这三条直线的斜率(k)计算出来。如果直线上有两点
利用上面的计算公式,分别把BC、BP、CP所在直线的斜率分别表示出来,然后进行分类讨论,利用两直线垂直斜率的积为-1建立等量关系,求解即可。
三、一线三垂直模型
一线三垂直模型这里就不赘述了,那么我们进行分类讨论。
1、当∠CPB为直角时,如图,过点P作y轴的垂线,交y轴于点D,过B点作x轴的垂线,两垂线相交于点E,那么这里就出现了相似三角形,△DCP∽△EPB。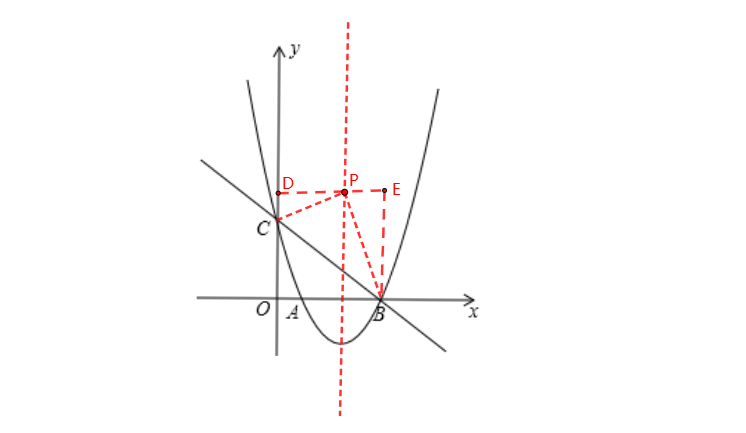
2、当∠PCB为直角时,如图,过点P作y轴的垂线,交y轴于点D,那么△DPC∽△OCB。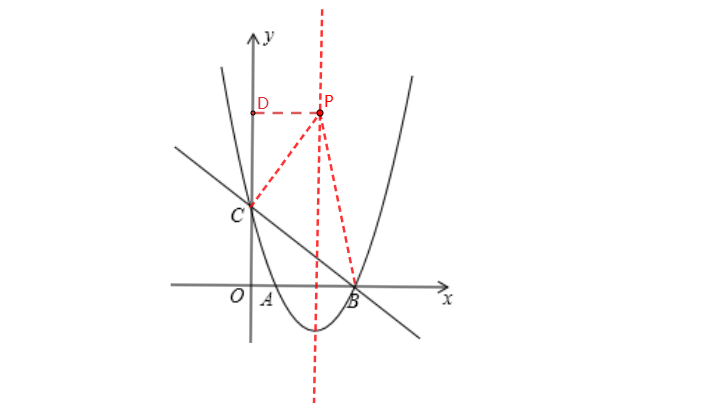
3、当∠CBP为直角时,如图,过点B作x轴的垂线,过点C作y轴的垂线,交于点D,过点P作x轴平行线,交DB所在直线于点E,这里又出现了一线三垂直模型,即△DCB∽EBP。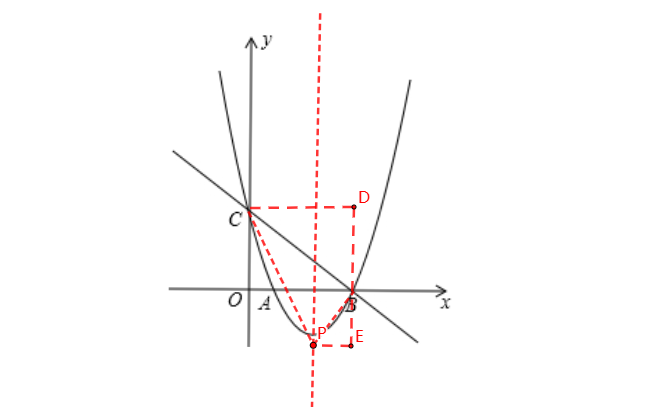
利用相似比建立等量关系,即可求出P点的坐标。
后续我们将利用这三种方法来求解上面例题和一道练习题。
 相似三角形是初中几何中非常重要的内容,常常与其他知识点结合,是中考的常考题型。本节主要介绍相似三角形模型——A字型和8字型模型
相似三角形是初中几何中非常重要的内容,常常与其他知识点结合,是中考的常考题型。本节主要介绍相似三角形模型——A字型和8字型模型 人教版数学九年级上册第二十二章《二次函数》知识点:二次函数概念,二次函数y=ax^2,y=ax^2+k,y=a(x-h)^2,y=a(x-h)^2+k,y=ax^2+bx+c图象和性质
人教版数学九年级上册第二十二章《二次函数》知识点:二次函数概念,二次函数y=ax^2,y=ax^2+k,y=a(x-h)^2,y=a(x-h)^2+k,y=ax^2+bx+c图象和性质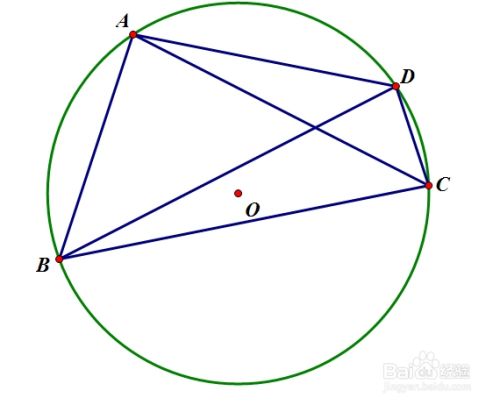 四点共圆:若在同一个平面内,有四个点在同一个圆上,则称这四个点共圆,一般简称“四点共圆”.
四点共圆:若在同一个平面内,有四个点在同一个圆上,则称这四个点共圆,一般简称“四点共圆”.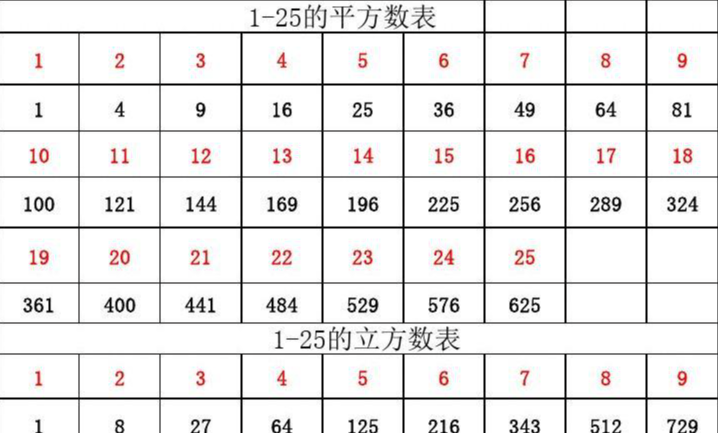 熟记常用数的平方和立方,对后期学习开平方和开立方奠定坚实的基础.
熟记常用数的平方和立方,对后期学习开平方和开立方奠定坚实的基础. 默认情况下 pip 使用的是国外的镜像,在下载的时候速度非常慢,本文我们介绍使用国内源对pip进行加速。
默认情况下 pip 使用的是国外的镜像,在下载的时候速度非常慢,本文我们介绍使用国内源对pip进行加速。 快速生成表格
快速生成表格 打包出现如下错误:Error: Application entry file "dist\electron\main.js" in the "D:\gui\demo2\build\win-unpacked\resources\app.asar" does not exist. Seems like a wrong configuration.
打包出现如下错误:Error: Application entry file "dist\electron\main.js" in the "D:\gui\demo2\build\win-unpacked\resources\app.asar" does not exist. Seems like a wrong configuration. Docker编译镜像出现:fetch http://dl-cdn.alpinelinux.org/alpine/v3.12/main/x86_64/APKINDEX.tar.gz
ERROR: http://dl-cdn.alpinelinux.org/alpine/v3.12/main: temporary error (try again later)
WARNING: Ignoring APKINDEX.2c4ac24e.tar.gz: No such file or directory问题
Docker编译镜像出现:fetch http://dl-cdn.alpinelinux.org/alpine/v3.12/main/x86_64/APKINDEX.tar.gz
ERROR: http://dl-cdn.alpinelinux.org/alpine/v3.12/main: temporary error (try again later)
WARNING: Ignoring APKINDEX.2c4ac24e.tar.gz: No such file or directory问题 在Mac电脑中,如何对Git的用户名和密码进行修改呢?起初不懂Mac,所以整了很久,本文将记录如何对这个进行操作,以便后期使用。
在Mac电脑中,如何对Git的用户名和密码进行修改呢?起初不懂Mac,所以整了很久,本文将记录如何对这个进行操作,以便后期使用。 在使用Git的过程中,不想每次都输入用户名和密码去拉取代码,所以就需要保存这些信息,那么既然有保存了,就必须有清除功能。
在使用Git的过程中,不想每次都输入用户名和密码去拉取代码,所以就需要保存这些信息,那么既然有保存了,就必须有清除功能。